题目内容
9.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过F2的直线交双曲线的渐近线于A、B两点,若F1A⊥F2A,且$\overrightarrow{{F}_{2}B}$=3$\overrightarrow{A{F}_{2}}$,则双曲线的离心率为( )| A. | 3 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
分析 设过F2的直线为y=k(x-c),双曲线的渐近线方程为y=±$\frac{b}{a}$x,联立方程组,求得A,B的坐标,运用向量共线的坐标表示和直线垂直的条件,结合双曲线的a,b,c,和离心率公式,计算即可得到所求.
解答 解:设过F2的直线为y=k(x-c),
双曲线的渐近线方程为y=±$\frac{b}{a}$x,
由$\left\{\begin{array}{l}{y=k(x-c)}\\{y=\frac{b}{a}x}\end{array}\right.$可得A($\frac{kac}{ka-b}$,$\frac{kbc}{ka-b}$),
由$\left\{\begin{array}{l}{y=k(x-c)}\\{y=-\frac{b}{a}x}\end{array}\right.$可得B($\frac{kac}{ka+b}$,-$\frac{kbc}{ka+b}$),
又F2(c,0),
由$\overrightarrow{{F}_{2}B}$=3$\overrightarrow{A{F}_{2}}$,可得3(c-($\frac{kac}{ka-b}$)=$\frac{kac}{ka+b}$-c,
化简可得ka=-2b,①
又F1A⊥F2A,
则$\frac{\frac{kbc}{ka-b}}{\frac{kac}{ka-b}+c}$=-$\frac{1}{k}$,即为kb2=b-2ka,②
由①②消去k,可得5a2=4b2,
由a2-b2=c2,
可得9a2=4c2,
则离心率e=$\frac{c}{a}$=$\frac{3}{2}$.
点评 本题考查双曲线的方程和性质,主要是渐近线方程和离心率的求法,考查向量共线的坐标表示和垂直的条件,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
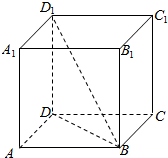 在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值.
在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值.