题目内容
14.已知$\left\{\begin{array}{l}{2x+y-2≥0}\\{x-2y+4≥0}\\{3x-y-3≤0}\end{array}\right.$,当x,y取何值时,x2+y2取得最大值,最小值?最大值,最小值各是多少?分析 由题意作出其平面区域,x2+y2可看成阴影部分内的点到原点的距离的平方,从而解最值.
解答 解:由题意作出其平面区域,
x2+y2可看成阴影部分内的点到原点的距离的平方,由图可知,
当取点B时有最大值,
由y=3x-3与x=2y-4联立解得,
x=2,y=3;即B(2,3);
所以当x=2,y=3时,x2+y2的最大值为22+32=13,
原点到直线y=-2x+2的距离的平方是其最小值,
d=$\frac{2}{\sqrt{4+1}}=\frac{2\sqrt{5}}{5}$,
所以x2+y2最小值是$(\frac{2}{\sqrt{5}})^{2}=\frac{4}{5}$,由$\left\{\begin{array}{l}{y=-2x+2}\\{y=\frac{1}{2}x}\end{array}\right.$解得x=$\frac{4}{5}$,y=$\frac{2}{5}$,即x=$\frac{4}{5}$,y=$\frac{2}{5}$时,x2+y2的最小值为$\frac{4}{5}$.
点评 本题考查了简单线性规划,关键是作图要细致认真,利用目标函数的几何意义求最值;属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过F2的直线交双曲线的渐近线于A、B两点,若F1A⊥F2A,且$\overrightarrow{{F}_{2}B}$=3$\overrightarrow{A{F}_{2}}$,则双曲线的离心率为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
6.阅读如图的程序框图,运行相应的程序,则输出i的值( )
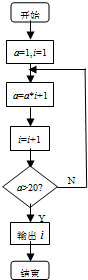

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1、F2,且椭圆E过点(0,$\sqrt{3}$),($\sqrt{3}$,-$\frac{\sqrt{6}}{2}$),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△${\;}_{A{F}_{1}{F}_{2}}$=$\sqrt{3}$.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个焦点为F1、F2,且椭圆E过点(0,$\sqrt{3}$),($\sqrt{3}$,-$\frac{\sqrt{6}}{2}$),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△${\;}_{A{F}_{1}{F}_{2}}$=$\sqrt{3}$.