题目内容

17．设椭圆$\frac{{x}^{2}}{m+48}$+$\frac{{y}^{2}}{m}$=1与直线x-y-3=0交于A（x1，y1），B（x2，y2）两点，求x1x2+y1y2的值．

分析 可联立直线方程和椭圆的方程消去x便可得到：（2m+48）y2+6my-m2-39m=0，根据韦达定理即可求出y1+y2，y1y2，而根据x1x2=（y1+3）（y2+3）即可得出x1x2，从而得出x1x2+y1y2．

解答 解：由$\left\{\begin{array}{l}{\frac{{x}^{2}}{m+48}+\frac{{y}^{2}}{m}=1}\\{x=y+3}\end{array}\right.$得：（2m+48）y2+6my-m2-39m=0；
∴${y}_{1}+{y}_{2}=-\frac{3m}{m+24}，{y}_{1}{y}_{2}=-\frac{{m}^{2}+39m}{2m+48}$；
∴x1x2=（y1+3）（y2+3）=y1y2+3（y1+y2）+9；
∴x1x2+y1y2=2y1y2+3（y1+y2）+9=$-\frac{{m}^{2}+39m}{m+24}-\frac{9m}{m+24}+9$=$-\frac{{m}^{2}+48m}{m+24}+9$．

点评 考查椭圆的标准方程，直线和椭圆的交点坐标和直线方程与椭圆方程形成方程组解的关系，以及韦达定理．

练习册系列答案
相关题目
6．求函数y=$\frac{1}{2}$$\sqrt{{x}^{2}+2x-3}$的单调区间．
7．已知f（x）=alnx，g（x）=-x2+3x-2．
（1）当a=1时，求f（x），g（x）在x=1处的切线；
（2）讨论函数h（x）=f（x）-g（x）的单调性；
（3）若f（x）＞g（x）在x＞1时恒成立，求a的取值范围．
5．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的两个焦点为F1、F2，且椭圆E过点（0，$\sqrt{3}$），（$\sqrt{3}$，-$\frac{\sqrt{6}}{2}$），点A是椭圆上位于第一象限的一点，且△AF1F2的面积S△${\;}_{A{F}_{1}{F}_{2}}$=$\sqrt{3}$．
（1）求点A的坐标；
（2）过点B（3，0）的直线l与椭圆E相交于点P、Q，直线AP、AQ分别与x轴相交于点M、N，点C（$\frac{5}{2}$，0），证明：|CM|•|CN|为定值，并求出该定值．
12．已知在极坐标下曲线C：ρ（cosθ+2sinθ）=4与点A（2，$\frac{π}{3}$），求曲线C与点A的位置关系．
2．在直角坐标系中，圆C的方程是x2+y2-4x=0，圆心为C，在以坐标原点为极点，以x轴的非负半轴为极轴建立的极坐标系中，曲线C1：ρ=-4$\sqrt{3}$sinθ与圆C相交于A，B两点．
（1）求直线AB的极坐标方程；
（2）若过点C（2，0）的直线C2：$\left\{\begin{array}{l}{x=2+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$（t是参数）交直线AB于点D，交y轴于点E，求|CD|：|CE|的值．
9．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2，过F2的直线交双曲线的渐近线于A、B两点，若F1A⊥F2A，且$\overrightarrow{{F}_{2}B}$=3$\overrightarrow{A{F}_{2}}$，则双曲线的离心率为（　　）
A．3B．$\frac{3}{2}$C．$\sqrt{3}$D．$\sqrt{6}$
6．阅读如图的程序框图，运行相应的程序，则输出i的值（　　）
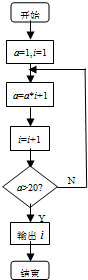
A．3B．4C．5D．6
7．f（x）=$\sqrt{4-x}$的定义域为（　　）
A．（4，+∞）B．（-∞，4]C．[4，+∞）D．（-∞，4）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网