题目内容
【题目】如图,三棱柱![]() 的侧面
的侧面![]() 是平行四边形,
是平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 分别是
分别是![]() 的中点.
的中点.

(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)当点![]() 是线段
是线段![]() 的中点时,
的中点时,![]() 平面
平面![]() .此时,
.此时,![]()
【解析】
(Ⅰ)由![]() ,利用面面垂直的性质,证得
,利用面面垂直的性质,证得![]() 平面
平面![]() ,在线面垂直的性质,即可得到
,在线面垂直的性质,即可得到![]() .
.
(Ⅱ)取![]() 中点
中点![]() ,连
,连![]() 连
连![]() ,得到四边形
,得到四边形![]() 为平行四边形,又由
为平行四边形,又由![]() 是
是![]() 的中点,证得
的中点,证得![]() ,且
,且![]() ,进而得到
,进而得到![]() ,利用线面平行的判定定理,即可证得
,利用线面平行的判定定理,即可证得![]() 平面
平面![]() .
.
(Ⅲ)取![]() 的中点
的中点![]() ,连
,连![]() ,连
,连![]() ,由线面垂直的性质,得到
,由线面垂直的性质,得到![]()
![]() ,
,![]()
![]() ,又在在△
,又在在△![]() 中,利用中位线得
中,利用中位线得![]() ,再由(Ⅱ)知
,再由(Ⅱ)知![]() ,进而得到
,进而得到![]() 平面
平面![]() ,得出结论.
,得出结论.
(Ⅰ)因为![]() ,又平面
,又平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)取![]() 中点
中点![]() ,连
,连![]() 连
连![]() .
.
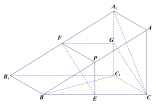
在△![]() 中,因为
中,因为![]() 分别是
分别是![]() 中点,
中点,
所以![]() ,且
,且![]() .
.
在平行四边形![]() 中,因为
中,因为![]() 是
是![]() 的中点,
的中点,
所以![]() ,且
,且![]() .
.
所以![]() ,且
,且![]() .
.
所以四边形![]() 是平行四边形.
是平行四边形.
所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅲ)在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() .
.
取![]() 的中点
的中点![]() ,连
,连![]() ,连
,连![]() .
.
因为![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,
所以![]()
![]() ,
,![]()
![]() .
.
在△![]() 中,因为
中,因为![]() 分别是
分别是![]() 中点,所以
中点,所以![]() .
.
又由(Ⅱ)知![]() ,
,
所以![]()
![]() ,
,![]() .
.
由![]()
![]() 得
得![]() 平面
平面![]() .
.
故当点![]() 是线段
是线段![]() 的中点时,
的中点时,![]() 平面
平面![]() .此时,
.此时,![]() .
.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目


