题目内容
定义方程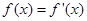 的实数根
的实数根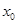 叫做函数
叫做函数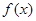 的“新驻点”,若函数
的“新驻点”,若函数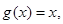
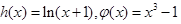 的“新驻点”分别为
的“新驻点”分别为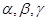 ,则
,则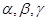 的大小关系为
的大小关系为
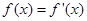 的实数根
的实数根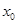 叫做函数
叫做函数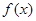 的“新驻点”,若函数
的“新驻点”,若函数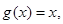
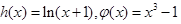 的“新驻点”分别为
的“新驻点”分别为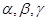 ,则
,则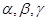 的大小关系为
的大小关系为A.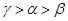 | B.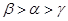 | C.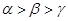 | D.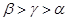 |
A
试题分析:
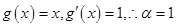 ,
,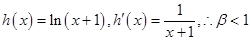 ,
,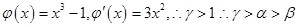
点评:在求函数新筑点时需解方程
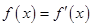 ,将其转化为函数
,将其转化为函数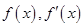 的交点横坐标,通过图像找到其范围比较大小
的交点横坐标,通过图像找到其范围比较大小
练习册系列答案
相关题目
题目内容
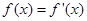 的实数根
的实数根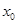 叫做函数
叫做函数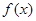 的“新驻点”,若函数
的“新驻点”,若函数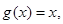
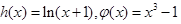 的“新驻点”分别为
的“新驻点”分别为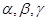 ,则
,则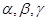 的大小关系为
的大小关系为A.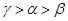 | B.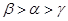 | C.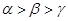 | D.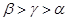 |
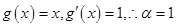 ,
,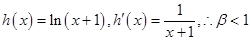 ,
,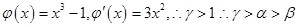
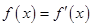 ,将其转化为函数
,将其转化为函数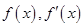 的交点横坐标,通过图像找到其范围比较大小
的交点横坐标,通过图像找到其范围比较大小