题目内容
已知函数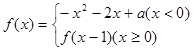 ,且函数
,且函数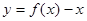 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数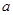 的取值范围是
的取值范围是
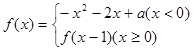 ,且函数
,且函数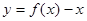 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数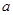 的取值范围是
的取值范围是A.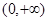 | B.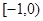 | C.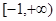 | D. |
C
试题分析:因为当x≥0的时候,f(x)=f(x-1),所以所有大于等于0的x代入得到的
f(x)相当于在[-1,0)重复的周期函数,
x∈[-1,0)时,
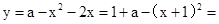 ,对称轴x=-1,顶点(-1,1+a)
,对称轴x=-1,顶点(-1,1+a)(1)如果a<-1,函数y=f(x)-x至多有2个不同的零点;
(2)如果a=-1,则y有一个零点在区间(-1,0),有一个零点在(-∞,-1),一个零点是原点;
(3)如果a>-1,则有一个零点在(-∞,-1),y右边有两个零点,
故实数a的取值范围是[-1,+∞)
故选C.
点评:典型题,本题通过分析函数的特征,明确其为周期函数,从而对函数图象有了全面认识,确定了函数零点所在区间。分类讨论思想的应用是关键。

练习册系列答案
相关题目
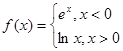 ,则
,则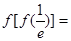 ____________
____________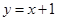
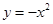
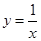
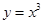
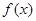 是定义在
是定义在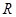 上的偶函数,且
上的偶函数,且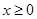 时,
时,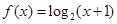 。
。 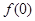 ,
,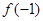 ;
;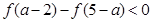 ,求
,求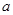 的取值范围。
的取值范围。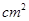 ,画面的宽与高的比为
,画面的宽与高的比为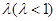 ,画面的上,下各留8
,画面的上,下各留8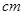 空白,左右各留5
空白,左右各留5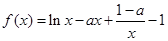
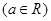 .
.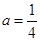 时①求
时①求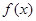 的单调区间;
的单调区间;  ,若对任意
,若对任意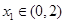 ,存在
,存在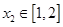 ,使
,使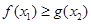 ,求实数
,求实数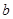 取值范围.
取值范围.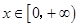 时,恒有
时,恒有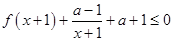 成立,求
成立,求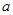 的取值范围.
的取值范围.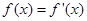 的实数根
的实数根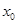 叫做函数
叫做函数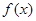 的“新驻点”,若函数
的“新驻点”,若函数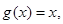
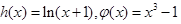 的“新驻点”分别为
的“新驻点”分别为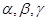 ,则
,则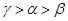
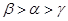
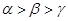
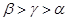
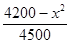 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).