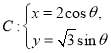题目内容
【题目】已知数列![]() 满足
满足![]() .
.
(1)若数列![]() 的首项为
的首项为![]() ,其中
,其中![]() ,且
,且![]() ,
,![]() ,
,![]() 构成公比小于0的等比数列,求
构成公比小于0的等比数列,求![]() 的值;
的值;
(2)若![]() 是公差为d(d>0)的等差数列
是公差为d(d>0)的等差数列![]() 的前n项和,求
的前n项和,求![]() 的值;
的值;
(3)若![]() ,
,![]() ,且数列
,且数列![]() 单调递增,数列
单调递增,数列![]() 单调递减,求数列
单调递减,求数列![]() 的通项公式.
的通项公式.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据![]() ,令
,令![]() ,再根据
,再根据![]() ,
,![]() ,
,![]() 构成公比小于0的等比数列,得到
构成公比小于0的等比数列,得到![]() ,联立求解.
,联立求解.
(2)根据![]() 是公差为d(d>0)的等差数列
是公差为d(d>0)的等差数列![]() 的前n项和,则由通项与前n项和的关系,得到
的前n项和,则由通项与前n项和的关系,得到![]() ,
,![]() ,再根据
,再根据![]() 对任意
对任意![]() 均成立,令
均成立,令![]() 联立求解.
联立求解.
(3)根据数列![]() 单调递增,数列
单调递增,数列![]() 单调递减,则有
单调递减,则有![]() ,
,![]() ,所以
,所以![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,两者联立求解.
,两者联立求解.
(1)由题意知: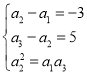 ,
,
所以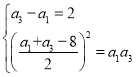 ,
,
解得:![]() ;
;
(2)由题意知:![]() ,
,![]() ,
,
所以![]() 对任意
对任意![]() 均成立,其中d>0,
均成立,其中d>0,
所以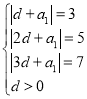 ,解得
,解得![]() ,
,
所以![]() .
.
此时,![]() 对任意
对任意![]() 均成立,故
均成立,故![]() ;
;
(3)由题意知:![]() ,
,![]() ,
,
故![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
则:![]() ,
,
故![]() ,
,
即n为奇数时,![]() ,
,
又n为奇数时,![]() ,所以
,所以![]() ,
,
即n为偶数时,![]() ,
,
综上,![]() .
.

【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
【题目】某地自2014年至2019年每年年初统计所得的人口数量如表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:千人) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)根据表中的数据判断从2014年到2019年哪个跨年度的人口增长数量最大?并描述该地人口数量的变化趋势;
(2)研究人员用函数![]() 拟合该地的人口数量,其中
拟合该地的人口数量,其中![]() 的单位是年,2014年年初对应时刻
的单位是年,2014年年初对应时刻![]() ,
,![]() 的单位是千人,经计算可得
的单位是千人,经计算可得![]() ,请解释
,请解释![]() 的实际意义.
的实际意义.