题目内容
【题目】已知函数![]() (
(![]() ,
,![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)若函数![]() 仅有一个极值点,求实数
仅有一个极值点,求实数![]() 的取值范围;
的取值范围;
(2)证明:当![]() 时,
时,![]() 有两个零点
有两个零点![]() (
(![]() ).且满足
).且满足![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:
(1)由函数的解析式可得![]() ,则满足题意时,方程
,则满足题意时,方程![]() 必无解,分类讨论:①当
必无解,分类讨论:①当![]() 时,符合题意;②当
时,符合题意;②当![]() 时,
时,![]() ,据此可得
,据此可得![]() .即实数
.即实数![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1)的结论可得,知当![]() 时,
时,![]() 为
为![]() 的唯一极小值点,且
的唯一极小值点,且![]() ,
,![]() ,则
,则![]() ,故
,故![]() .要证明
.要证明![]() ,即证
,即证![]() .,可转化为
.,可转化为![]() ,即
,即![]() ,据此构造函数
,据此构造函数![]() ,结合函数的性质可知
,结合函数的性质可知![]() 在区间
在区间![]() 上是减函数,
上是减函数,![]() ,等价于
,等价于![]() 成立,则原命题得证.
成立,则原命题得证.
试题解析:
(1)![]()
![]() ,
,
由![]() ,得
,得![]() 或
或![]()
因为![]() 仅有一个极值点,
仅有一个极值点,
所以关于![]() 的方程
的方程![]() 必无解,
必无解,
①当![]() 时,
时,![]() 无解,符合题意;
无解,符合题意;
②当![]() 时,由
时,由![]() ,得
,得![]() ,
,
故由![]() ,得
,得![]() .
.
故当![]() 时,若
时,若![]() ,
,
则![]() ,此时
,此时![]() 为减函数,
为减函数,
若![]() ,则
,则![]() ,此时
,此时![]() 为增函数,
为增函数,
所以![]() 为
为![]() 的唯一极值点,
的唯一极值点,
综上,可得实数![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1),知当![]() 时,
时,![]() 为
为![]() 的唯一极值点,且是极小值点,
的唯一极值点,且是极小值点,
又因为当![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,
所以当![]() 时,
时,![]() 有一个零点
有一个零点![]() ,
,
当![]() 时,
时,![]() 有另一个零点
有另一个零点![]() ,
,
即![]() ,
,
且![]() ,
,
![]() .①
.①
所以![]() .
.
下面再证明![]() ,即证
,即证![]() .
.
由![]() ,得
,得![]() ,
,
因为当![]() 时,
时,![]() 为减函数,
为减函数,
故只需证明![]() ,
,
也就是证明![]() ,
,
因为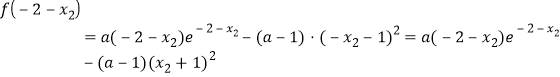 ,
,
由①式,
可得![]() .
.
令![]() ,
,
则![]() .
.
令![]() ,
,
因为![]() 为区间
为区间![]() 上的减函数,且
上的减函数,且![]() ,所以
,所以![]() ,即
,即![]()
在区间![]() 上恒成立,
上恒成立,
所以![]() 在区间
在区间![]() 上是减函数,即
上是减函数,即![]() ,所以
,所以![]() ,
,
即证明![]() 成立,
成立,
综上所述,![]() .
.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图。
分组 | 频数 | 频率 |
[50,60) | 2 | 0.04 |
[60,70) | 8 | 0.16 |
[70,80) | 10 | |
[80,90) | ||
[90,100] | 14 | 0.28 |
合计 | 1.00 |
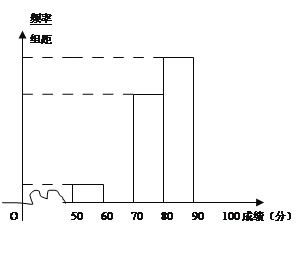
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)请你估算学生成绩的平均数及中位数。