题目内容
【题目】已知函数![]()
![]() 有极值,且函数
有极值,且函数![]() 的极值点是
的极值点是![]() 的极值点,其中
的极值点,其中![]() 是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
是自然对数的底数.(极值点是指函数取得极值时对应的自变量的值)
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() 时,若函数
时,若函数![]() 的最小值为
的最小值为![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ,
, ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)先分别求两函数极值点,再根据条件得![]() 关于
关于![]() 的函数关系式;最后求自变量取值范围(2)先研究
的函数关系式;最后求自变量取值范围(2)先研究![]() 导函数零点情况,仅有一个零点,再根据导函数符号变化规律确定最小值,最后再利用导数求最小值函数单调性,根据单调性证明不等式
导函数零点情况,仅有一个零点,再根据导函数符号变化规律确定最小值,最后再利用导数求最小值函数单调性,根据单调性证明不等式
试题解析:(1)因为![]()
![]() ,令
,令![]() ,解得
,解得![]() .
.
列表如下.
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以![]() 时,
时, ![]() 取得极小值.
取得极小值.
因为![]() ,
,
由题意可知![]() ,且
,且![]()
所以![]() ,
,
化简得![]() ,
,
由![]()
![]() ,得
,得![]() .
.
所以![]() ,
, ![]() .
.
(2)因为![]()
![]() ,
,
所以![]()
![]()
![]()
![]()
记![]() ,则
,则![]() ,令
,令![]() ,解得
,解得![]() .
.
列表如下.
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以![]() 时,
时, ![]() 取得极小值,也是最小值,
取得极小值,也是最小值,
此时, ![]()
![]()
![]()
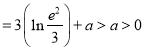 .
.
令![]() ,解得
,解得![]() .
.
列表如下.
|
|
|
|
|
|
|
|
|
| 极小值 |
|
所以![]() 时,
时, ![]() 取得极小值,也是最小值.
取得极小值,也是最小值.
所以![]()
![]()
![]() .
.
令![]() ,则
,则![]() ,
,
记![]()
![]() ,
, ![]() ,
,
则![]() ,
, ![]() .
.
因为![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() 单调递增.
单调递增.
所以![]() ,
,
所以![]() .
.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表如下,频率分布直方图如图:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[25,30)内的概率.