题目内容
1.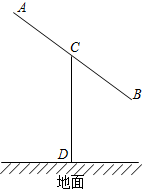 某建筑的金属支架如图所示,根据要求AB至少长2.8米,C为AB的中点,B到D的距离比CD的长小0.5米,$∠BCD=\frac{π}{3}$,若建筑支架各部分的材料每米的价格已确定,且AB部分的价格是CD部分价格的两倍.设BC=x米,CD=y米.
某建筑的金属支架如图所示,根据要求AB至少长2.8米,C为AB的中点,B到D的距离比CD的长小0.5米,$∠BCD=\frac{π}{3}$,若建筑支架各部分的材料每米的价格已确定,且AB部分的价格是CD部分价格的两倍.设BC=x米,CD=y米.(1)求y关于x的函数;
(2)问怎样设计AB的长,可使建造这个支架的成本最低?
分析 (1)由题意 BC=x,CD=y.连结BD,在△CDB中,利用余弦定理可得:化简整理即可得出:$y=\frac{{{x^2}-\frac{1}{4}}}{x-1}$.(x≥1.4)
(2)设金属支架CD每米价格为a元,金属支架AB每米价格为2a元,则总成本为y•a+2x•(2a)=a(y+4x)$y+4x=\frac{{{x^2}-\frac{1}{4}}}{x-1}+4x$,设$t=x-1,t≥\frac{2.8}{2}-1=0.4$,换元变形利用基本不等式的性质即可得出.
解答 解:(1)由题意 BC=x,CD=y.
连结BD,则在△CDB中,${(y-\frac{1}{2})^2}={y^2}+{x^2}-2xycos\frac{π}{3}$,
整理得:$y=\frac{{{x^2}-\frac{1}{4}}}{x-1}$.(x≥1.4)
(2)设金属支架CD每米价格为a元,金属支架AB每米价格为2a元,
则总成本为y•a+2x•(2a)=a(y+4x)$y+4x=\frac{{{x^2}-\frac{1}{4}}}{x-1}+4x$,
设$t=x-1,t≥\frac{2.8}{2}-1=0.4$,
则$y+4x=5t+\frac{3}{4t}+6$,
令$g(t)=5t+\frac{3}{4t}+6$,在[0.4,+∞)上单调增,
所以当t=0.4时,即x=1.4时,取得最小值.
答:当AB=2.8m时,建造这个支架的成本最低.
点评 本题考查了余弦定理、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.对于抛物线y=4x2,下列描述正确的是( )
| A. | 开口向上 | B. | 开口向下 | C. | 开口向左 | D. | 开口向右 |
6.关于x的方程lnx+x-2=0的根为x0,则x0所在区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
13.若关于x的方程x3-3x+a=0有三个不同的实数解,则实数a的取值范围( )
| A. | -2<a≤0 | B. | 0≤a<2 | C. | -2<a<2 | D. | -2≤a≤2 |
11.若0<a<1,-1<b<0,则函数y=ax+b的图象必不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |