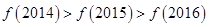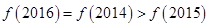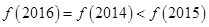题目内容
13.已知数列{an}是等差数列,若a3+a11=30,a4=9.(1)求an;
(2)若数列{an}的前n项和为Sn,且bn=$\frac{1}{S_n}$,证明:b1+b2+…+bn<$\frac{3}{4}$.
分析 (1)设等差数列{an}的公差为d,运用等差数列的通项公式,可得首项和公差,可得an;
(2)求得Sn,运用裂项相消求和求得{bn}的前n项和,即可得证.
解答 解:(1)设等差数列{an}的公差为d,
则a1+2d+a1+10d=30,a1+3d=9,
解得a1=3,d=2,
则an=3+2(n-1)=2n+1;
(2)Sn=$\frac{1}{2}$(3+2n+1)n=n2+2n,
即有bn=$\frac{1}{S_n}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
则b1+b2+…+bn=$\frac{1}{1×3}$+$\frac{1}{2×4}$+…+$\frac{1}{n(n+2)}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}-\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)<$\frac{3}{4}$.
点评 本题考查等差数列的通项和求和公式的运用,考查数列的求和方法:裂项相消求和,考查运算能力,属于中档题.

练习册系列答案
相关题目
5.一个算法程序如图所示,则输出的n的值为( )
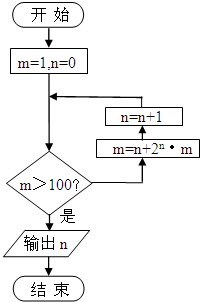

| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
4.将两颗骰子各掷一次,设事件A=“两个点数不相同”,B=“至少出现一个6点”,则概率P(A|B)等于( )
| A. | $\frac{10}{11}$ | B. | $\frac{5}{11}$ | C. | $\frac{5}{18}$ | D. | $\frac{5}{36}$ |
1.袋中装有5个小球,颜色分别是红色、黄色、白色、黑色和紫色,现从袋中随机抽取3个小球.设每个小球被抽到的机会均等,则抽到白球或黑球的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{9}{10}$ |
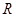 上的函数
上的函数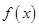 满足:①
满足:①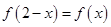 ;②
;②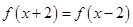 ;③当
;③当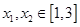 时,
时,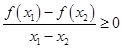 ,则
,则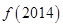 、
、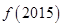 、
、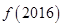 满足( )
满足( )