题目内容
9.下列四个函数中,在区间(0,$\frac{1}{4}$)上为减函数的是( )| A. | y=x($\frac{1}{2}$)x | B. | y=-($\frac{1}{2}$)x | C. | y=xlog2x | D. | y=x${\;}^{\frac{1}{3}}$ |
分析 A,C求函数的导数,利用导数研究函数的单调性,B,D利用指数函数和幂函数的单调性的性质进行判断.
解答 解:A.y=x($\frac{1}{2}$)x 求导得y′=($\frac{1}{2}$)x-x($\frac{1}{2}$)x•ln2=($\frac{1}{2}$)x(1-xln2),对于x∈(0,$\frac{1}{4}$),y′>0,
故y=x($\frac{1}{2}$)x在区间(0,$\frac{1}{4}$)上为增函数,
B.y=-($\frac{1}{2}$)x在(0,$\frac{1}{4}$)上是增函数,
C.函数的导数y′=log2x+$\frac{x}{xln2}$=log2x+$\frac{1}{ln2}$=log2x+log2e=log2ex,
∵0<x<$\frac{1}{4}$,
∴0<ex<$\frac{1}{4}$e<1,此时y′<0,
即在区间(0,$\frac{1}{4}$)上为减函数,满足条件.
D.y=x${\;}^{\frac{1}{3}}$在(0,$\frac{1}{4}$)上为增函数,
故选:C
点评 本题主要考查函数单调性的判断,要求熟练掌握掌握常见函数的单调性,对应复杂函数,利用导数研究函数的单调性是解决本题的关键.

练习册系列答案
相关题目
1.袋中装有5个小球,颜色分别是红色、黄色、白色、黑色和紫色,现从袋中随机抽取3个小球.设每个小球被抽到的机会均等,则抽到白球或黑球的概率为( )
| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{9}{10}$ |
 ,则
,则 ____________.
____________.  的六个顶点都在半径为1的半球面上,
的六个顶点都在半径为1的半球面上, ,侧面
,侧面 是半球底面圆的内接正方形,则侧面
是半球底面圆的内接正方形,则侧面 的面积为( )
的面积为( )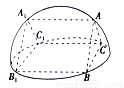
 D.
D.