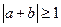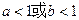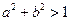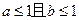题目内容

设p：实数x满足x2-4ax+3a2＜0，其中a＜0，q：实数x满足x2-x-12≤0或x2+2x-15＞0，且?p是?q的必要不充分条件，求实数a的取值范围．
由x2-x-12≤0解得x≥4或x≤-3．由x2+2x-15＞0，解得x＞3或x＜-5，此时x＞3或x≤-3，即q：x＞3或x≤-3．
由x2-4ax+3a2＜0，其中a＜0，得（x-a）（x-3a）＜0，所以3a＜x＜a，即p：3a＜x＜a．
因为?p是?q的必要不充分条件，即q是p的必要不充分条件，
所以a≤-3．
练习册系列答案
相关题目
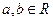若，则使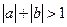成立的一个充分不必要条件是　　　（　）
A．B．C．D．
设x，y∈R，则“x≥2且y≥1”是“x2+y2≥4”的（　　）
A．充分但不必要条件B．必要但不充分条件
C．既不充分又不必要条件D．充要条件
设a＞0且a≠1，则“函数f（x）=ax在R上是减函数”，是“函数g（x）=（2-a）x3在R上是增函数”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件
已知条件p：
4x
x-3
＜1，条件q：5x-6＞x2，则p是q的（　　）
A．必要不充分条件B．充分不必要条件
C．充要条件D．既不充分也不必要条件
已知命题p：x2-7x+10≤0，命题q：x2-2x+（1-a）（1+a）≤0，（a＞0），若“￢p”是“￢q”的必要而不充分条件，求a的取值范围．
若集合M={-1，m2}，集合N={2，4}，则“m=2”是“M∩N={4}”的______．（填“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”）
命题甲：x≠1005或y≠1006；命题乙：x+y≠2011．则命题甲是命题乙的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分又不必要条件
“|x|=|y|”是“x2=y2的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网