题目内容
设a>0且a≠1,则“函数f(x)=ax在R上是减函数”,是“函数g(x)=(2-a)x3在R上是增函数”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
a>0a≠1,则“函数f(x)=ax在R上是减函数”,所以a∈(0,1),
“函数g(x)=(2-a)x3在R上是增函数”所以a∈(0,2);
显然a>0a≠1,则“函数f(x)=ax在R上是减函数”,
是“函数g(x)=(2-a)x3在R上是增函数”的充分不必要条件.
故选A.
“函数g(x)=(2-a)x3在R上是增函数”所以a∈(0,2);
显然a>0a≠1,则“函数f(x)=ax在R上是减函数”,
是“函数g(x)=(2-a)x3在R上是增函数”的充分不必要条件.
故选A.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
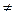 4, 命题乙:a
4, 命题乙:a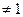 且b
且b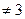 ,则命题甲是命题乙的 .
,则命题甲是命题乙的 .