Question

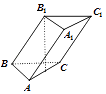
【题目】如图所示，在长方体中，为的中点，连接和.

（1）求证：平面平面；

（2）求二面角的正切值。

Answer 1

【答案】（1）见解析（2）

【解析】

（1）先由BC⊥平面D1DCC1BC⊥DE．再利用△DD1E为等腰直角三角形∠D1ED=45°以及∠C1EC=45°可得DE⊥EC，合在一起可得平面EDB⊥平面EBC；
（2）先过E在平面D1DCC1中作EO⊥DC于OEO⊥面ABCD；再O在平面DBC中作OF⊥DB于F，利用三垂线定理极其逆定理可得EF⊥BD．所以∠EFO为二面角E-DB-C的平面角．再利用平面几何知识求出∠EFO的正切值即可；

（1）证明：在长方体ABCD-A1B1C1D1中，
AB=2，BB1=BC=1，E为D1C1的中点．
∴△DD1E为等腰直角三角形，∠D1ED=45°．同理∠C1EC=45°．
∴∠DEC=90°，即DE⊥EC．
在长方体ABCD-A1B1C1D1中，BC⊥平面D1DCC1，又DE平面D1DCC1，
∴BC⊥DE．又EC∩BC=C，∴DE⊥平面EBC．
∵DE平面DEB，∵平面DEB⊥平面EBC．
（2）如图，过E在平面D1DCC1中作EO⊥DC于O．

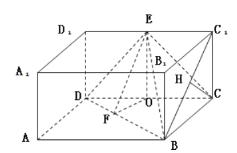
在长方体ABCD-A1B1C1D1中，∵面ABCD⊥面D1DCC1，∴EO⊥面ABCD．
过O在平面DBC中作OF⊥DB于F，
连接EF∴EF⊥BD．
∠EFO为二面角E-DB-C的平面角．
利用平面几何知识可得OF＝ OE＝1，tan∠EFO＝,

所以二面角E-DB-C的正切值为.