题目内容
已知函数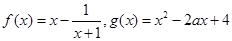 若对任意x1∈[0,1],存在x2∈[1,2],使
若对任意x1∈[0,1],存在x2∈[1,2],使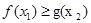 ,求实数a的取值范围?
,求实数a的取值范围?
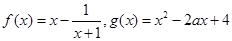 若对任意x1∈[0,1],存在x2∈[1,2],使
若对任意x1∈[0,1],存在x2∈[1,2],使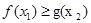 ,求实数a的取值范围?
,求实数a的取值范围?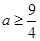
试题分析:根据题意可知,函数
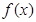 在
在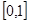 上的最小值得大于等于
上的最小值得大于等于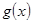 在
在 上的值,所以得求得函数
上的值,所以得求得函数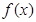 在
在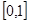 上的最小值,通过导数法,判断单调性得最小值;然后令
上的最小值,通过导数法,判断单调性得最小值;然后令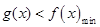 ,建立关于
,建立关于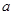 的不等式,设出新的函数
的不等式,设出新的函数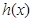 ,探讨与
,探讨与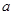 的关系,从而得出满足条件的实数
的关系,从而得出满足条件的实数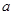 .
.试题解析:根据
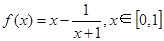 ,求导可得
,求导可得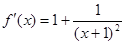 ,
,显然
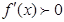 ,所以函数
,所以函数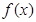 在
在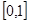 上单调递增.所以
上单调递增.所以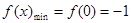
根据题意可知存在
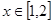 ,使得
,使得 ,
,即
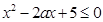 即
即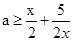 能成立,
能成立,令
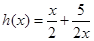 ,则要使
,则要使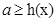 ,在
,在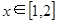 能成立,只需使
能成立,只需使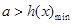 ,
,又函数
 中,
中,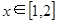 ,求导可得
,求导可得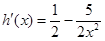 .当
.当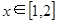 时,显然
时,显然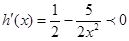 ,所以函数
,所以函数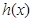 在
在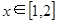 上单调递减.
上单调递减.所以
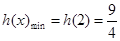 ,故只需
,故只需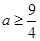 .
.
练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
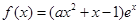 ,其中
,其中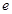 是自然对数的底数,
是自然对数的底数, .
. ,求曲线
,求曲线 在点
在点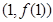 处的切线方程;
处的切线方程; ,求
,求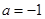 ,函数
,函数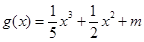 的图像有3个不同的交点,求实数
的图像有3个不同的交点,求实数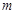 的取值范围.
的取值范围.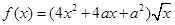 ,其中
,其中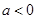 .
.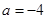 时,求
时,求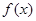 的单调递增区间;
的单调递增区间;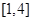 上的最小值为8,求
上的最小值为8,求 的值.
的值.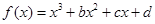 的图象过点P(0,2),且在点M(-1,
的图象过点P(0,2),且在点M(-1,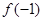 )处的切线方程
)处的切线方程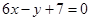 。
。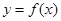 的解析式;
的解析式; 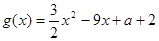 与
与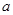 的取值范围。
的取值范围。 在区间
在区间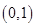 上单调递增,且方程
上单调递增,且方程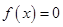 的根都在区间
的根都在区间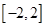 上,则实数b的取值范围为( )
上,则实数b的取值范围为( )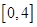

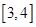
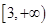
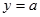 与函数
与函数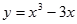 的图像有三个相异的交点,则
的图像有三个相异的交点,则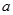 的取值范围为( )
的取值范围为( )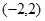
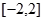
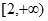

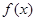 ,
,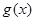 分别是定义在
分别是定义在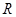 上的奇函数和偶函数,当
上的奇函数和偶函数,当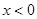 时,
时,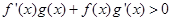 ,且
,且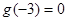 ,则不等式
,则不等式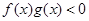 的解集是 ( )
的解集是 ( )



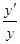 =φ′(x)·ln f(x)+φ(x)·
=φ′(x)·ln f(x)+φ(x)· ,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·
,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·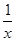 的单调递增区间是________.
的单调递增区间是________.