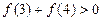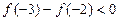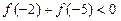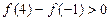题目内容
已知f(x)是定义在[-1,1]上的奇函数. 当a, b∈[-1,1],且a+b≠0时,有
(1)判断函数f(x)的的单调性,并给以证明;
(2)若f(1)=1,且f(x)≤m2-2bm+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数m的取值范围.

(1)判断函数f(x)的的单调性,并给以证明;
(2)若f(1)=1,且f(x)≤m2-2bm+1对所有x∈[-1,1],b∈[-1,1]恒成立,求实数m的取值范围.
(1)见解析(2)(-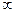 ,-2]∪{0}∪[2,+
,-2]∪{0}∪[2,+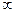 )
)
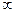 ,-2]∪{0}∪[2,+
,-2]∪{0}∪[2,+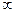 )
)(1)证明:设x1,x2∈[-1,1],且x1<x2,
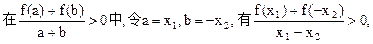
∵x1<x2,∴x1-x2<0,又∵f(x)是奇数,∴f(-x2)=-f(x2),

即f(x1)< f(x2).故f(x)在[-1,1]上为增函数.
(2)解:∵f(1)=1且f(x )在[-1,1]上为增函数,所以对x∈[-1,1],有f(x)≤f(1)=1.由题意,对所有的x∈[-1,1],b∈[-1,1],有f(x)≤m2-2bm+1恒成立,
所以m2-2bm+1≥1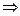 m2-2bm≥0.
m2-2bm≥0.
记g(b)=-2mb+m2,对所有的b∈[-1,1],要g(b)≥0恒成立.只需
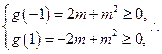 m∈(-
m∈(-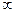 ,-2]∪{0}∪[2,+
,-2]∪{0}∪[2,+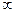 ).
).
所以实数m的取值范围是:m∈(-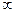 ,-2]∪{0}∪[2,+
,-2]∪{0}∪[2,+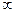 ).
).
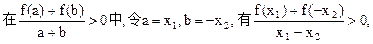
∵x1<x2,∴x1-x2<0,又∵f(x)是奇数,∴f(-x2)=-f(x2),

即f(x1)< f(x2).故f(x)在[-1,1]上为增函数.
(2)解:∵f(1)=1且f(x )在[-1,1]上为增函数,所以对x∈[-1,1],有f(x)≤f(1)=1.由题意,对所有的x∈[-1,1],b∈[-1,1],有f(x)≤m2-2bm+1恒成立,
所以m2-2bm+1≥1
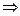 m2-2bm≥0.
m2-2bm≥0.记g(b)=-2mb+m2,对所有的b∈[-1,1],要g(b)≥0恒成立.只需
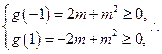 m∈(-
m∈(-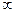 ,-2]∪{0}∪[2,+
,-2]∪{0}∪[2,+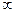 ).
).所以实数m的取值范围是:m∈(-
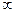 ,-2]∪{0}∪[2,+
,-2]∪{0}∪[2,+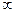 ).
).
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
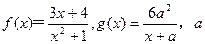 >
>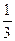 ,
,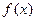 的极大值与极小值;
的极大值与极小值;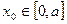 ,总存在相应的
,总存在相应的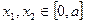 ,使得
,使得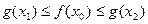 成立,求实数a的取值范围.
成立,求实数a的取值范围.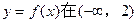 上为增函数,且函数
上为增函数,且函数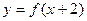 的图象的对称轴为
的图象的对称轴为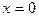 ,则( )
,则( )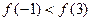

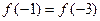
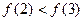
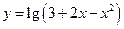 的定义域为集合
的定义域为集合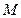 ,求:当
,求:当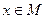 时,函数
时,函数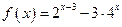 的最值,并指出
的最值,并指出 取得最值时的
取得最值时的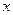 值.
值.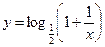 在区间
在区间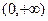 上是( )
上是( )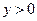
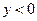
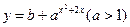 在区间
在区间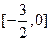 上有最大值3,最小值
上有最大值3,最小值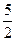 ,试求
,试求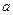 和
和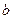 的值
的值
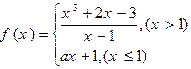 在点
在点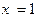 处连续,则
处连续,则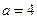 ;
;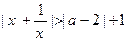 对于一切非零实数
对于一切非零实数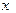 均成立,则实数
均成立,则实数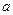 的取值范围是
的取值范围是 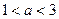
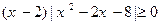 的解集是
的解集是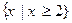
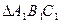 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于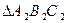 的三个内角的正弦值,则
的三个内角的正弦值,则 若函数
若函数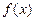 是定义在
是定义在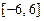 上的偶函数,且在
上的偶函数,且在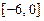 上单调递减,则( ).
上单调递减,则( ).