题目内容
a≤-
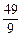
由log2(x+3)+log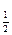 x≤3得
x≤3得
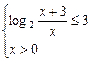
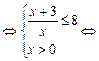 x≥
x≥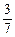 ,
,
即f(x)的定义域为[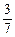 ,+∞).
,+∞).
∵f(x)在定义域[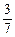 ,+∞)内单调递减,
,+∞)内单调递减,
∴当x2>x1≥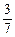 时,f(x1)-f(x2)>0恒成立,即有(ax1-
时,f(x1)-f(x2)>0恒成立,即有(ax1-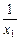 +2)-(ax2-
+2)-(ax2-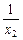 +2)
+2)
>0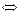 a(x1-x2)-(
a(x1-x2)-(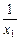 -
-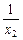 )>0
)>0
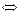 (x1-x2)(a+
(x1-x2)(a+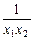 )>0恒成立.
)>0恒成立.
∵x1<x2,∴(x1-x2)(a+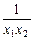 )>0
)>0
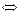 a+
a+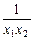 <0.
<0.
∵x1x2>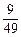
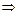 -
-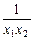 >-
>-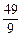 ,
,
要使a<-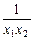 恒成立,
恒成立,
则a的取值范围是a≤-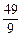 .
.
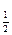 x≤3得
x≤3得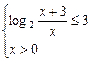
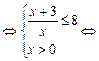 x≥
x≥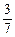 ,
,即f(x)的定义域为[
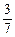 ,+∞).
,+∞).∵f(x)在定义域[
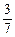 ,+∞)内单调递减,
,+∞)内单调递减,∴当x2>x1≥
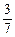 时,f(x1)-f(x2)>0恒成立,即有(ax1-
时,f(x1)-f(x2)>0恒成立,即有(ax1-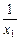 +2)-(ax2-
+2)-(ax2-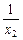 +2)
+2)>0
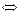 a(x1-x2)-(
a(x1-x2)-(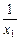 -
-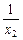 )>0
)>0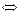 (x1-x2)(a+
(x1-x2)(a+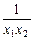 )>0恒成立.
)>0恒成立.∵x1<x2,∴(x1-x2)(a+
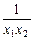 )>0
)>0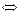 a+
a+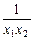 <0.
<0.∵x1x2>
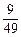
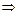 -
-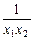 >-
>-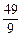 ,
,要使a<-
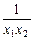 恒成立,
恒成立,则a的取值范围是a≤-
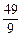 .
.
练习册系列答案
相关题目

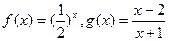 ,试判断H(x)=f(-2x)+g(x)在
,试判断H(x)=f(-2x)+g(x)在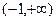 的单调性并加以证明
的单调性并加以证明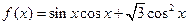
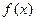 的最小正周期;
的最小正周期;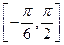 上的最大值和最小值
上的最大值和最小值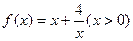
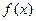 在
在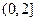 上的单调性,并用定义证明;
上的单调性,并用定义证明;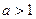 ,求
,求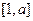 上的最大值
上的最大值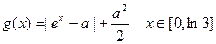 ,求函数
,求函数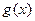 的最小值
的最小值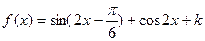
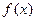 的单调递增区间;
的单调递增区间;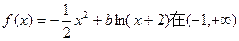 上是减函数,则b的取值范围是
上是减函数,则b的取值范围是

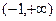

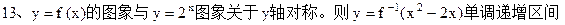 为( )
为( )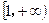 B
B 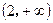 C
C 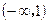 D
D