题目内容
【题目】如图,已知斜三棱柱ABC﹣A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°. 
(1)求证:BC⊥AB1;
(2)若AB=2,AB1= ![]() ,求二面角C﹣AB1﹣C1(锐角)的余弦值.
,求二面角C﹣AB1﹣C1(锐角)的余弦值.
【答案】
(1)证明:∵四边形BB1C1C是菱形,∠CBB1=60°,
∴△BB1C是等边三角形,
取BC的中点为O,连结OA,OB,则BC⊥OB1,
又∵△ABC是等边三角形,∴BC⊥OA,
∵OA∩OB1,∴BC⊥平面AOB1,
∵AB1平面AOB1,∴BC⊥AB1.
(2)解:∵△ABC和△BB1C是全等的等边三角形,AB=2,
∴OA=OB1= ![]() ,
,
又∵AB1= ![]() ,∴
,∴ ![]() ,∴OB1⊥OA,
,∴OB1⊥OA,
又∵OB1⊥BC,∴OB1⊥平面ABC,
分别以OA,OB,OB1所在的直线作为x,y,z轴,建立空间直角坐标系,
则A( ![]() ),B(0,1,0),C(0,﹣1,0),
),B(0,1,0),C(0,﹣1,0),
![]() =(0,﹣1,﹣
=(0,﹣1,﹣ ![]() ),
), ![]() =(﹣
=(﹣ ![]() ),
), ![]() =(0,﹣2,0),
=(0,﹣2,0), ![]() =(﹣
=(﹣ ![]() ,﹣1,0),
,﹣1,0),
设 ![]() =(x,y,z)是平面C1AB1的一个法向量,
=(x,y,z)是平面C1AB1的一个法向量,
则  ,取x=1,得
,取x=1,得 ![]() =(1,0,1),
=(1,0,1),
设 ![]() =(a,b,c)是平面CAB1的一个法向量,
=(a,b,c)是平面CAB1的一个法向量,
则 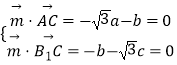 ,取a=1,得
,取a=1,得 ![]() =(1,﹣
=(1,﹣ ![]() ,1),
,1),
cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
∴二面角C﹣AB1﹣C1(锐角)的余弦值为 ![]() .
.
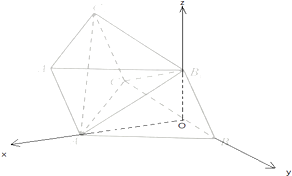
【解析】(1)推导出△BB1C是等边三角形,取BC的中点为O,则BC⊥OB1 , 由△ABC是等边三角形,得BC⊥OA,从而BC⊥平面AOB1 , 由此能证明BC⊥AB1 . (2)分别以OA,OB,OB1所在的直线作为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣AB1﹣C1(锐角)的余弦值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.

 名校课堂系列答案
名校课堂系列答案【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
储蓄存款 | 6 | 7 | 8 | 9 | 10 |
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)用所求回归方程预测该地区2015年![]() 的人民币储蓄存款.
的人民币储蓄存款.
附:回归方程![]() 中,
中, 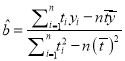 ,
,