题目内容
【题目】《数书九章》是中国南宋时期杰出数学家秦九韶的著作，其中在卷五“三斜求积”中提出了已知三角形三边
、
、
，求面积的公式，这与古希腊的海伦公式完全等价，其求法是“以小斜冥并大斜冥减中斜冥，余半之，自乘于上，以小斜冥乘大斜冥减上，余四约之，为实．一为从隅，开平方得积”若把以上这段文字写出公式，即若
，则
．
（1）已知
的三边，，，且，求证：的面积．
（2）若
，
，求的面积
的最大值．
【答案】（1）见解析；（2）
【解析】
（1）由三角形的面积公式和同角的平方关系、余弦定理可得证明；
（2）运用两角和的正切公式，求得
，再由余弦定理和基本不等式，结合三角形的面积公式可得所求最大值．
（1）
，
，
；
（2）由
，可得
，
即有
，
由
，可得
，
，
即有
，即
，
由于
，故
，由余弦定理可得
，
可得
，当且仅当
时取得等号，则
的面积
，即
的最大值为．
阳光课堂同步练习系列答案
【题目】“双十一”期间，某淘宝店主对其商品的上架时间
（小时）和销售量
（件）的关系作了统计，得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
（1）求表中销售量
的平均数和中位数；
（2）① 作出散点图，并判断变量
与
是否线性相关？若研究的方案是先根据前5组数据求线性回归方程，再利用第6组数据进行检验，求线性回归方程
；
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件，则认为得到的线性回归方程是理想的，试问：①中的线性回归方程是否理想.
附：线性回归方程
中，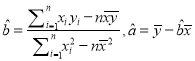 
.
【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.
