Question

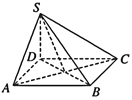
【题目】如图，在四棱锥P-ABCD中，AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD，PA⊥AD.E和F分别是CD和PC的中点，求证：

（1）PA⊥底面ABCD;

（2）平面BEF⊥平面PCD.

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】试题分析：（1）根据条件，易证四边形是平行四边形，所以，平面，平面，所以平面；

（2）由条件易证平面，，所以平面，，根据中点，，所以，，那么可证明平面，平面，根据面面垂直的判定定理，平面平面．

试题解析：证明：（1）因为平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，所以PA⊥底面ABCD．

因为AB∥CD，CD=2AB，E为CD的中点，所以AB∥DE，且AB=DE．

所以ABED为平行四边形，所以BE∥AD．

又因为平面PAD，AD平面PAD，所以BE∥平面PAD．

（2）因为AB⊥AD，而且ABED为平行四边形，所以BE⊥CD，AD⊥CD．

由（1）知PA⊥底面ABCD，所以PA⊥CD，因为PAAD=A，

所以CD⊥平面PAD，所以CD⊥PD．

因为E和F分别是CD和PC的中点，所以PD∥EF，所以CD⊥EF．

又EFBE=E，所以CD⊥平面BEF．

所以平面BEF⊥平面PCD．