题目内容
14.已知等差数列{an}满足${a_3}=7,{a_5}+{a_7}=26,{b_n}=\frac{1}{{{a_n}^2-1}}(n∈{N^*})$,数列{bn}的前n项和为Sn,则S100的值为( )| A. | $\frac{101}{25}$ | B. | $\frac{35}{36}$ | C. | $\frac{25}{101}$ | D. | $\frac{3}{10}$ |
分析 利用已知条件求出等差数列{an}的通项公式,然后化简${b}_{n}=\frac{1}{{{a}_{n}}^{2}-1}$,利用裂项求和,求解即可.
解答 解:在等差数列{an}中,a5+a7=2a6=26⇒a6=13,又数列{an}的公差$d=\frac{{{a_6}-{a_3}}}{6-3}=\frac{13-7}{3}=2$,
所以an=a3+(n-3)d=7+(n-3)×2=2n+1,
那么${b_n}=\frac{1}{{{a_n}^2-1}}=\frac{1}{4n(n+1)}=\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$,
故Sn=b1+b2+…+bn=$\frac{1}{4}(1-\frac{1}{n+1})⇒{S_{100}}=\frac{1}{4}(1-\frac{1}{101})=\frac{25}{101}$
故选:C.
点评 本题考查数列的递推关系式的应用,数列求和,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知全集U=R,集合A={x|y=log3(x-1)},B={y|y=2x},则(∁∪A)∩B=( )
| A. | (0,+∞) | B. | (0,1] | C. | (1,+∞) | D. | (1,2) |
19.在等腰△ABC中,角A,B,C的对边分别为a,b,c,若sinB=sinAcosC-$\frac{1}{2}$sinC,且a=$\sqrt{3}$,则△ABC的面积为( )
| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | ||
| C. | $\sqrt{3}$ | D. | 条件不足,无法计算 |
6.正三棱柱的正视图的面积是8(如图所示),则侧视图的面积为( )


| A. | 4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 2$\sqrt{3}$ |
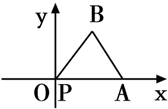 将边长为2的等边△PAB沿x轴正方向滚动,某时刻P与坐标原点重合(如图),设顶点P(x,y)的轨迹方程是y=f(x),关于函数y=f(x)的有下列说法:
将边长为2的等边△PAB沿x轴正方向滚动,某时刻P与坐标原点重合(如图),设顶点P(x,y)的轨迹方程是y=f(x),关于函数y=f(x)的有下列说法: