题目内容
4.已知点O是正方体ABCD-A′B′C′D′的对角线AC的中点,过B′作B′H⊥D′O于点H,求证:B′H⊥平面ACD′.分析 连结BD,AC交点即为O,连结BD,先利用线面垂直的性质证明出AC⊥BB′,然后推断出AC⊥BD,进而利用线面垂直的判定定理证明出AC⊥面BDD′B′,则可推断出AC⊥B′H,进而根据已知条件和线面垂直的判定定理证明出B′H⊥平面ACD′.
解答 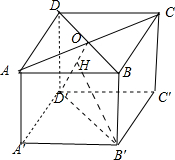 证明:连结BD,AC交点即为O,连结BD,
证明:连结BD,AC交点即为O,连结BD,
由题意知BB′⊥面ABCD,
∵AC?面ABCD,
∴AC⊥BB′,
∵ABCD为正方形,
∴AC⊥BD,
∵BD?面ABCD,BB′?面ABCD,BD∩BB′=B,
∴AC⊥面BDD′B′,
∵B′H?面BDD′B′,
∴AC⊥B′H,
∵B′H⊥D′O,D′O?平面ACD′,AC平面ACD′,AC∩OD=O,
∴B′H⊥平面ACD′.
点评 本题主要考查了线面垂直的判定定理的运用.要求学生能熟练掌握判定定理的内容并能灵活运用.

练习册系列答案
相关题目
15. 已知一空间几何体的三视图如题图所示,其中正视图与左视图都是全等的等腰梯形,则该几何体的体积为( )
已知一空间几何体的三视图如题图所示,其中正视图与左视图都是全等的等腰梯形,则该几何体的体积为( )
 已知一空间几何体的三视图如题图所示,其中正视图与左视图都是全等的等腰梯形,则该几何体的体积为( )
已知一空间几何体的三视图如题图所示,其中正视图与左视图都是全等的等腰梯形,则该几何体的体积为( )| A. | 17 | B. | $\frac{52}{3}$ | C. | $\frac{55}{3}$ | D. | 18 |
15.已知|$\overrightarrow{a}$|=2$\sqrt{10}$,$\overrightarrow{b}$=(-1,3),且$\overrightarrow{a}•\overrightarrow{b}$=10,则向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
12.已知等差数列{an}前n项和为Sn,a4=2,S10=10,则a7的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13.已知函数f(x)=sin2ωx+$\sqrt{3}$sinωx•cosωx,α∈R,又f(α)=-$\frac{1}{2}$,f(β)=$\frac{1}{2}$.若|α-β|的最小值为$\frac{3π}{4}$,则正数ω的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
14.已知等差数列{an}满足${a_3}=7,{a_5}+{a_7}=26,{b_n}=\frac{1}{{{a_n}^2-1}}(n∈{N^*})$,数列{bn}的前n项和为Sn,则S100的值为( )
| A. | $\frac{101}{25}$ | B. | $\frac{35}{36}$ | C. | $\frac{25}{101}$ | D. | $\frac{3}{10}$ |