题目内容
19．将甲，乙等5位同学分别保送到北京大学，复旦大学，中国科技大学就读，则每所大学至少保送一人的不同保送的方法数共有（ ）种．| A． | 240 | B． | 180 | C． | 150 | D． | 540 |
分析 每所大学至少保送一人，可以分类来解，当5名学生分成2，2，1时，共有$\frac{1}{2}$C52C32A33，当5名学生分成3，1，1时，共有$\frac{1}{2}$C53${C}_{2}^{1}$A33，根据分类计数原理得到结果．
解答 解：当5名学生分成2，2，1或3，1，1两种形式，
当5名学生分成2，2，1时，共有$\frac{1}{2}$C52C32A33=90种结果，
当5名学生分成3，1，1时，共有$\frac{1}{2}$C53${C}_{2}^{1}$A33=60种结果，
∴根据分类计数原理知共有90+60=150种，
故选：C．
点评 本题考查了分组分配问题，关键是如何分组，属于中档题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
9．已知 F1，F2分别是双曲线 $\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左，右焦点，过 F1，的直线l与双曲线的左右两支分别交于点A，B，若|AB|=|AF2|，∠F1AF2=90°，则双曲线的离心率为（ ）
| A． | $\frac{{\sqrt{6}+\sqrt{3}}}{2}$ | B． | $\sqrt{6}+\sqrt{3}$ | C． | $\frac{{\sqrt{5+2\sqrt{2}}}}{2}$ | D． | $\sqrt{5+2\sqrt{2}}$ |
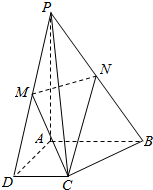如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，∠BAD=∠CDA=90°，PA⊥平面ABCD，PA=AD=AB=2，CD=1，M，N分别是PD，PB的中点．