题目内容
15.已知|$\overrightarrow{a}$|=2$\sqrt{10}$,$\overrightarrow{b}$=(-1,3),且$\overrightarrow{a}•\overrightarrow{b}$=10,则向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 根据向量的数量积公式解答.
解答 解:已知|$\overrightarrow{a}$|=2$\sqrt{10}$,$\overrightarrow{b}$=(-1,3),则|$\overrightarrow{b}$|=$\sqrt{10}$,且$\overrightarrow{a}•\overrightarrow{b}$=10,则向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角的余弦值为:$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{10}{2\sqrt{10}\sqrt{10}}=\frac{1}{2}$,向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角范围为[0,180°],
所以向量$\overrightarrow{a}$与向量$\overrightarrow{b}$的夹角为60°;
故选:B.
点评 本题考查了利用数量积公式求向量的夹角;属于基础题.

练习册系列答案
相关题目


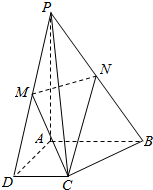 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD,PB的中点.