题目内容
某大学志愿者协会有6名男同学,4名女同学.在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院.现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(1)求选出的3名同学是来自互不相同学院的概率;
(2)设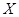 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量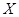 的分布列和数学期望.
的分布列和数学期望.
(1)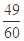 ;(2)随机变量
;(2)随机变量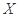 的分布列为
的分布列为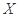
0 1 2 3 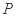
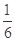
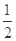
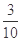
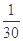
数学期望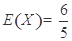 .
.
解析试题分析:(1)由已知可知选出的3名同学可能有1名来自数学学院,其余2名同学来自物理、化学等其他互不相同的七个学院,或者3名同学都来自物理、化学等其他互不相同的七个学院,由互斥事件的概率加法公式即可求得“选出的3名同学是来自互不相同学院的概率”;(2)首先,随机变量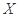 的所有可能值为0,1,2,3.而随机变量
的所有可能值为0,1,2,3.而随机变量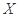 服从超几何分布,可先分别求出
服从超几何分布,可先分别求出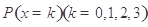 的值,最后利用公式即可求得随机变量
的值,最后利用公式即可求得随机变量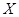 的分布列和数学期望.
的分布列和数学期望.
(1)设“选出的3名同学来自互不相同的学院”为事件 ,则
,则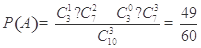 ,∴选出的3名同学来自互不相同学院的概率为
,∴选出的3名同学来自互不相同学院的概率为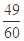 .
.
(2)随机变量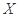 的所有可能值为0,1,2,3.
的所有可能值为0,1,2,3.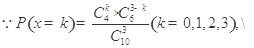 随机变量
随机变量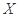 的分布列为
的分布列为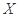
0 1 2 3 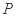
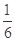
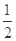
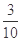
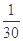
随机变量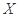 的数学期望
的数学期望 .
.
考点:1.古典概型及其概率计算公式;2.互斥事件;3.离散型随机变量的分布列与数学期望.

练习册系列答案
相关题目
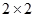 列联表:
列联表: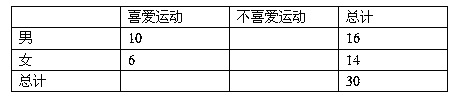
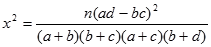 (其中
(其中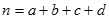 )
)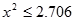
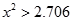

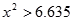
 .
.
 ,
, ,
, ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取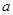 ,
,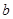 ,
,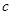 .
.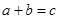 ”的概率;
”的概率; ,第二次出现的点数为
,第二次出现的点数为 .
.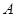 为“
为“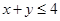 ”,求
”,求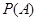 ;
;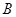 为“
为“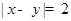 ”,求
”,求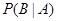 .
.
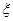 ,求
,求 .
.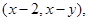 记
记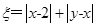 .
. 的最大值,并求事件“
的最大值,并求事件“