题目内容
某电视台“挑战60秒”活动规定上台演唱:
(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).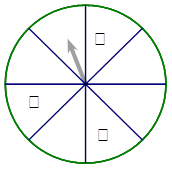
(2)转盘指针落在I、II、III区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.
(3)演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒.
①求此人中一等奖的概率;
②设此人所得奖金为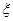 ,求
,求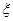 的分布列及数学期望
的分布列及数学期望 .
.
(1) 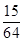 (2)200
(2)200
解析试题分析:(1)由题意可知转一次奖获得一等奖的概率是 ,分成三类情况:①两次都中中一等奖②第一次中一等奖,第二次未中;③第一次未中一等奖,第二次中;
,分成三类情况:①两次都中中一等奖②第一次中一等奖,第二次未中;③第一次未中一等奖,第二次中;
(2)分别计算出奖金为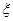 每一种情况的概率,然后列出分布列,再计算出期望值即可.
每一种情况的概率,然后列出分布列,再计算出期望值即可.
解: ①
②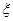
0 100 200 300 400 500 600 700 1000 
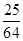
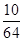
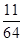


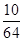



故
考点:相互独立事件的概率;离散型随机变量的分布列和数学期望

练习册系列答案
相关题目
某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
| API | 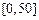 | 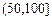 | 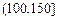 | 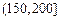 | 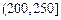 | 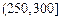 | 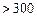 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中度重污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为ω。在区间[0,100]对企业没有造成经济损失;在区间
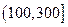 对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;
对企业造成经济损失成直线模型(当API为150时造成的 经济损失为500元,当API为200时,造成的经济损失为700元);当API大于300时造成的 经济损失为2000元;(1)试写出是S(ω)的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失S大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?
|
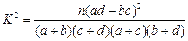
| | 非重度污染 | 重度污染 | 合计 |
| 供暖季 | | | |
| 非供暖季 | | | |
| 合计 | | | 100 |
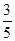 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是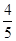 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用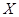 表示张同学答对题的个数,求
表示张同学答对题的个数,求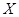 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量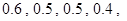 各人是否需使用设备相互独立.
各人是否需使用设备相互独立. ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验.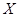 的概率分布列和期望.
的概率分布列和期望.  个元素的总体
个元素的总体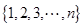 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体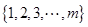 和
和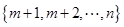 (
(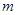 是给定的正整数,且
是给定的正整数,且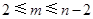 ),再从每个子总体中各随机抽取
),再从每个子总体中各随机抽取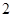 个元素组成样本.用
个元素组成样本.用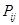 表示元素
表示元素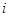 和
和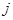 同时出现在样本中的概率.
同时出现在样本中的概率.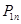 的表达式(用
的表达式(用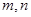 表示);
表示);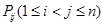 的和.
的和.