题目内容
将一颗质地均匀的正四面体骰子(四个面的点数分别为1,2,3,4)先后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 .
.
(1)记事件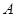 为“
为“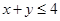 ”,求
”,求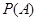 ;
;
(2)记事件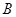 为“
为“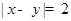 ”,求
”,求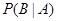 .
.
(1)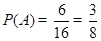 ;(2)
;(2)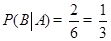 .
.
解析试题分析:(1)先用穷举法得到先后抛掷两次,出现点数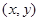 的基本事件总数
的基本事件总数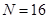 ,从中找出满足
,从中找出满足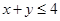 的事件数
的事件数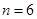 ,根据古典概型的概率计算公式即可得到所求的概率
,根据古典概型的概率计算公式即可得到所求的概率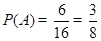 ;(2)在
;(2)在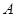 事件发生的前提下,找出事件
事件发生的前提下,找出事件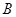 包含的事件数
包含的事件数 ,进而可得条件概率
,进而可得条件概率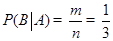 .
.
(1)投掷骰子2次得到的所有结果为: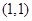 ,
,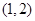 ,
,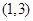 ,
,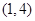 ,
,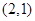 ,
,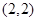 ,
,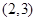 ,
,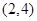 ,
,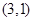 ,
,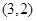 ,
,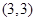 ,
,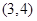 ,
,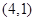 ,
,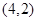 ,
,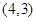 ,
,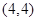 共16种 2分
共16种 2分
事件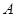 包含的结果有:
包含的结果有: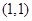 ,
,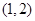 ,
,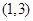 ,
,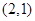 ,
,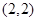 ,
,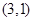 共6种 4分
共6种 4分
则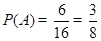 6分
6分
(2)在事件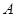 发生的前提下,事件
发生的前提下,事件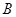 包含的结果有:
包含的结果有: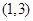 ,
,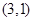 (共2种) 10分
(共2种) 10分
则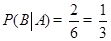 13分.
13分.
考点:1.古典概率;2.条件概率.

练习册系列答案
相关题目
有甲、乙两个班进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 总计 | | | 210 |
已知从全部210人中随机抽取1人为优秀的概率为
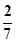 .
.(1)请完成上面的2×2列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”.
附:
 ,其中
,其中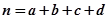 .
.| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; | |
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; | |
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
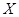 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量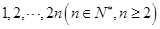 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为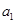 ,最大数为
,最大数为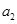 ;B组最小数为
;B组最小数为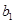 ,最大数为
,最大数为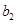 ,记
,记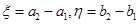
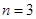 时,求
时,求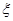 的分布列和数学期望;
的分布列和数学期望;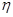 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率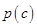 ;
;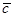 表示C的对立事件,判断
表示C的对立事件,判断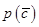 的大小关系,并说明理由。
的大小关系,并说明理由。 各人是否需使用设备相互独立.
各人是否需使用设备相互独立. ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验.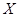 的概率分布列和期望.
的概率分布列和期望. 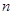 个黑球(
个黑球(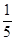 ,求
,求