题目内容
(本小题满分12分)一个盒子里装有三张卡片,分别标记有数字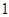 ,
,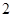 ,
,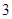 ,这三张卡片除标记的数字外完全相同。随机有放回地抽取
,这三张卡片除标记的数字外完全相同。随机有放回地抽取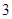 次,每次抽取
次,每次抽取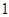 张,将抽取的卡片上的数字依次记为
张,将抽取的卡片上的数字依次记为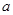 ,
,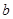 ,
,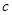 .
.
(Ⅰ)求“抽取的卡片上的数字满足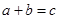 ”的概率;
”的概率;
(Ⅱ)求“抽取的卡片上的数字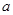 ,
,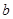 ,
,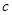 不完全相同”的概率.
不完全相同”的概率.
(1)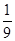 ;(2)
;(2)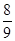 .
.
解析试题分析:共有9张卡片,有放回地取3次,则每次都有9种选择,将所有可能结果一一列举出来,共有27种不同的结果.(1)满足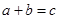 的结果包括
的结果包括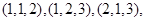 ,共3种,故所求概率为
,共3种,故所求概率为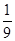 ;(2)根据正难则反的原则,我们可以先考虑其对立事件,即
;(2)根据正难则反的原则,我们可以先考虑其对立事件,即 完全相同的结果,它包括
完全相同的结果,它包括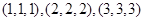 ,共3种,故所求概率为
,共3种,故所求概率为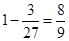 .
.
试题解析:(1)由题意得,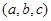 的所有可能为:
的所有可能为: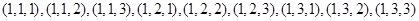 ,
,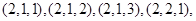
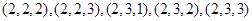 ,
,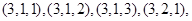
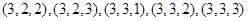 ,共27种.
,共27种.
设“抽取的卡片上的数字满足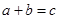 ”为事件A,则事件A包括
”为事件A,则事件A包括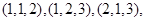 ,共3种,
,共3种,
所以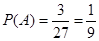 .
.
因此“抽取的卡片上的数字满足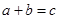 ”的概率为
”的概率为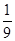
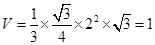 .
.
(2)设“抽取的卡片上的数字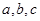 不完全相同”为事件B,
不完全相同”为事件B,
则事件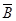 包括
包括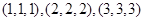 ,共3种,
,共3种,
所以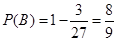 .
.
因此“抽取的卡片上的数字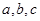 不完全相同”的概率为
不完全相同”的概率为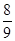 .
.
【考点定位】古典概型及随机事件的概率.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示: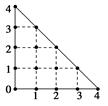
| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望.
 分).学科网设每次击鼓出现音乐的概率为
分).学科网设每次击鼓出现音乐的概率为 ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立. ,求
,求 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量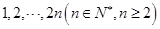 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为 ,最大数为
,最大数为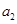 ;B组最小数为
;B组最小数为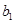 ,最大数为
,最大数为 ,记
,记
 时,求
时,求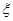 的分布列和数学期望;
的分布列和数学期望; 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率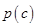 ;
; 表示C的对立事件,判断
表示C的对立事件,判断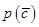 的大小关系,并说明理由。
的大小关系,并说明理由。 为甲、乙、丙这三个学生选修数学史这门课的人数,求
为甲、乙、丙这三个学生选修数学史这门课的人数,求