题目内容
(本题满分16分)已知数列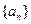 的前
的前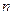 项和为
项和为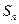 ,且
,且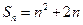 .数列
.数列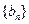 中,
中,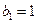 ,
,
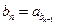
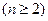 .(1)求数列
.(1)求数列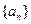 的通项公式;(2)若存在常数
的通项公式;(2)若存在常数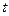 使数列
使数列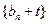 是等比数列,求数列
是等比数列,求数列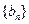 的通项公式;(3)求证:①
的通项公式;(3)求证:①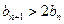 ;②
;②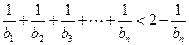 .
.
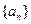 的前
的前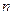 项和为
项和为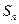 ,且
,且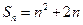 .数列
.数列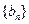 中,
中,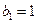 ,
,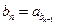
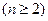 .(1)求数列
.(1)求数列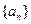 的通项公式;(2)若存在常数
的通项公式;(2)若存在常数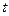 使数列
使数列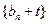 是等比数列,求数列
是等比数列,求数列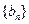 的通项公式;(3)求证:①
的通项公式;(3)求证:①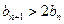 ;②
;②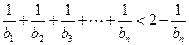 .
.(Ⅰ) 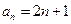 (Ⅱ)
(Ⅱ) 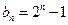 (Ⅲ)略
(Ⅲ)略
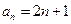 (Ⅱ)
(Ⅱ) 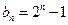 (Ⅲ)略
(Ⅲ)略:(Ⅰ)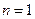 时,
时,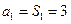 ,
,
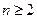 时,
时,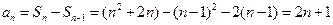 , -------2分
, -------2分
且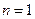 时也适合此式,故数列
时也适合此式,故数列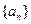 的通项公式是
的通项公式是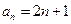 ;
; ------3分
------3分
(Ⅱ)依题意,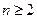 时,
时,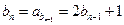 ,
,
∴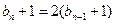 ,又
,又 ,-----6分
,-----6分
∴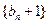 是以2为首项,2为公比的等比数列,即存在常数
是以2为首项,2为公比的等比数列,即存在常数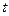 =2使数列
=2使数列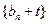 是等比数列
是等比数列
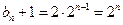 ,即
,即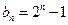 . -------8分
. -------8分

 (Ⅲ) ①
(Ⅲ) ①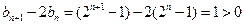 所以
所以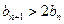 对一切自然数
对一切自然数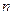 都成立10分
都成立10分
②由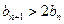 得
得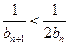 设
设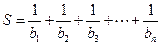
则S 13分
13分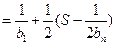
所以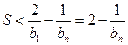 . -----16分
. -----16分
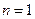 时,
时,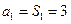 ,
,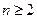 时,
时,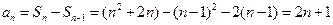 , -------2分
, -------2分且
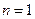 时也适合此式,故数列
时也适合此式,故数列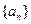 的通项公式是
的通项公式是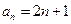 ;
; ------3分
------3分(Ⅱ)依题意,
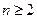 时,
时,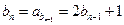 ,
,∴
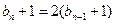 ,又
,又 ,-----6分
,-----6分∴
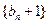 是以2为首项,2为公比的等比数列,即存在常数
是以2为首项,2为公比的等比数列,即存在常数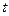 =2使数列
=2使数列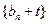 是等比数列
是等比数列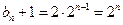 ,即
,即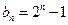 . -------8分
. -------8分
 (Ⅲ) ①
(Ⅲ) ①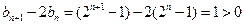 所以
所以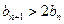 对一切自然数
对一切自然数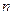 都成立10分
都成立10分②由
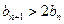 得
得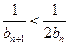 设
设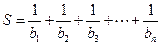
则S
 13分
13分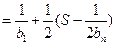
所以
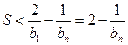 . -----16分
. -----16分
练习册系列答案
相关题目

 的单调区间;
的单调区间;
 上的最小值为
上的最小值为 令
令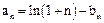 ;
;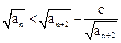 恒成立,求实数c的取值范围;
恒成立,求实数c的取值范围;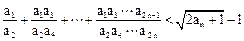 。
。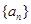 满足
满足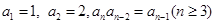 ,则
,则 的值为 ( )
的值为 ( )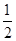
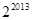
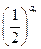 .已知b1+b2+b3=
.已知b1+b2+b3=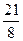 , b1b2b3=
, b1b2b3=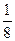 .求等差数列的通项an.
.求等差数列的通项an.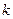 棵树种植在点
棵树种植在点 处,其中
处,其中 ,当
,当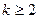 时,
时,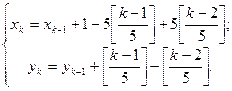 其中,
其中,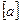 表示实数
表示实数 的整数部分,例如
的整数部分,例如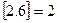 ,
,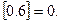 按此方案,第2008棵树种植点的坐标为 .
按此方案,第2008棵树种植点的坐标为 .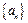 的前n项的和Sn,满足
的前n项的和Sn,满足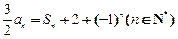 .
.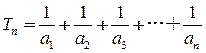 ,是否存在正整数k,使得当n≥3时,
,是否存在正整数k,使得当n≥3时,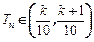 如果存在,求出k;如果不存在,请说明理由.
如果存在,求出k;如果不存在,请说明理由. 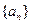 中,
中,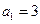 ,前
,前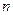 项和为
项和为 ,等比数列
,等比数列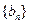 各项均为正数,
各项均为正数, ,且
,且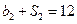 ,
,
 (1)求
(1)求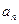 与
与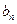 ;(2)证明:
;(2)证明: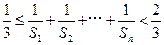
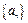 中,
中,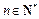 ,若
,若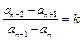 (
(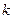 为常数),则称
为常数),则称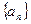 中,已知
中,已知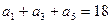 ,
,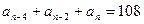 ,S
,S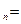 420,则
420,则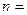 .
.