题目内容
10.函数y=(sin2x)2的周期为$\frac{π}{2}$.分析 由条件利用半角公式化简函数的解析式,再根据y=Acos(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,得出结论.
解答 解:函数y=(sin2x)2 =$\frac{1-cos4x}{2}$=$\frac{1}{2}$-$\frac{1}{2}$cos4x的周期为$\frac{2π}{4}$=$\frac{π}{2}$,
故答案为:$\frac{π}{2}$.
点评 本题主要考查半角公式,三角函数的周期性及其求法,利用了y=Acos(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,属于基础题.

练习册系列答案
相关题目
20.由曲线y=x2,y=x围成的封闭图形的面积为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
18.下列函数中,在其定义域内既是偶函数又在(-∞,0)上单调递增的函数是( )
| A. | f(x)=x2 | B. | f(x)=-log2|x| | C. | f(x)=3|x| | D. | f(x)=sinx |
15.执行如图所示的程序框图,输出的结果为( )
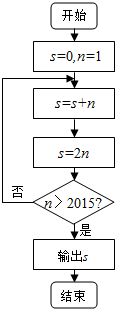

| A. | 210-1 | B. | 211-1 | C. | 21007-1 | D. | 21024-1 |
19.已知抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,其中a、b、c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,记随机变量X=|a-b|,则X的均值EX为( )
| A. | $\frac{8}{9}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{3}$ |