题目内容
【题目】设a∈R,函数f(x)=|x2﹣2ax|,方程f(x)=ax+a的四个实数解满足x1<x2<x3<x4 .
(1)求a的取值范围;
(2)证明:f(x4)> ![]() +8
+8 ![]() .
.
【答案】
(1)解:若a=0,则f(x)=x2,显然直线y=ax+a与f(x)不可能有4个交点,不符合题意;
若a<0,作出f(x)=|x2﹣2ax|的函数图象,则直线y=ax+a与f(x)的图象不可能有4个交点,不符合题意;
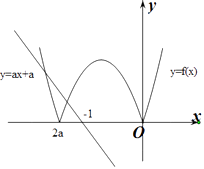
若a>0,作出f(x)的函数图象如图所示:
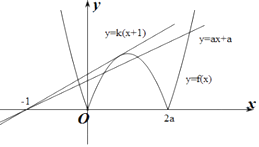
当0<x<2a时,f(x)=﹣x2+2ax,
设直线y=k(x+1)与y=f(x)在(0,2a)上的函数图象相切,切点为(x0,y0),
则 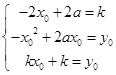 ,解得k=2a+2﹣2
,解得k=2a+2﹣2 ![]() ,
,
∴a<2a+2﹣2 ![]() ,解得a>4
,解得a>4
(2)解:联立方程组 ![]() ,得x2﹣3ax﹣a=0,解得x=
,得x2﹣3ax﹣a=0,解得x= ![]() ,
,
∴x4= ![]() .
.
∴f(x4)=ax4+a= ![]() +
+ ![]() +a,
+a,
令g(a)= ![]() +
+ ![]() +a,则g(a)在(4,+∞)上单调递增,
+a,则g(a)在(4,+∞)上单调递增,
∴g(a)>g(4)=28+8 ![]() >
> ![]() +8
+8 ![]() .
.
∴f(x4)> ![]() +8
+8 ![]()
【解析】(1)根据f(x)的图象与直线y=ax+a有4个交点可知a>0,利用导数求出f(x)的过点(﹣1,0)的切线斜率,列出不等式得出a的范围;(2)求方程组,用a表示出x4,得出f(x4)关于a的函数,利用单调性得出结论.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目