题目内容
16.如图,正方体ABCD-A1B1C1D1的棱长为2,E,F,G分别是B1C1,AD1,D1E的中点.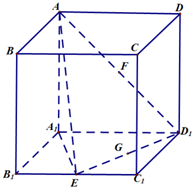
(1)求证:FG∥平面AA1E;
(2)求FG与平面A1B1C1D1所成的角的正切值.
分析 (Ⅰ)证明FG∥AE,通过直线与平面平行的判定定理证明FG∥平面AA1E.
(Ⅱ)取A1D1的中点H,连接FH、HG,说明∠FGH为直线FG与平面${A_1}{B_1}{C_1}D_1^{\;}$所成的角,在直角△FGH中,求解tan∠FGH即可.
解答 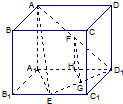 满分(12分).
满分(12分).
(Ⅰ)证明:∵F为AD1的中点,且G为D1E的中点
∴FG为△AED1的中位线∴FG∥AE----------------------(2分)
又∵FG?平面AA1E,AE?平面AA1E,∴FG∥平面AA1E---------------------(5分)
(Ⅱ)解:取A1D1的中点H,连接FH、HG
∵FH为△A1D1A的中位线,∴FH∥$AA_1^{\;}$-------------------------------(6分)
又∵$AA_1^{\;}⊥$平面${A_1}{B_1}{C_1}D_1^{\;}$,∴FH⊥平面${A_1}{B_1}{C_1}D_1^{\;}$------------------------------(8分)
∴∠FGH为直线FG与平面${A_1}{B_1}{C_1}D_1^{\;}$所成的角------------(9分)
在直角△AB1E1中,A1E=$\sqrt{{A_1}{B_1}^2+{B_1}{E^2}}$=$\sqrt{5}$
∵GH是△A1ED1的中位线,∴GH=$\frac{{{A_1}E}}{2}$=$\frac{{\sqrt{5}}}{2}$------------------------------(10分)
又∵FH=$\frac{{A{A_1}}}{2}$=1,∴在直角△FGH中,tan∠FGH=$\frac{{2\sqrt{5}}}{5}$------------------(11分)
故直线FG与平面${A_1}{B_1}{C_1}D_1^{\;}$所成的角的正切值为$\frac{{2\sqrt{5}}}{5}$------(12分)
点评 本题考查空间线面位置关系、角的计算等基础知识,考查空间想象能力、运算求解能力、推理论证能力,考查化归与转化等数学思想.

| A. | 2 | B. | -2 | C. | ±2 | D. | $\sqrt{5}$ |
| A. | $\frac{1}{32}$a,32b | B. | 32a,$\frac{1}{32}b$ | C. | 16a,$\frac{1}{32}b$ | D. | 16a,$\frac{1}{16}b$ |
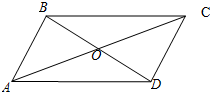 如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.
如图,在平行四边形ABCD中,BD,AC相交于点O,设向量$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$.