题目内容
1.在△ABC中,E为边AC上一点,且$\overrightarrow{AC}$=3$\overrightarrow{AE}$,P为BE上一点,且满足$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$(m>0,n>0),则$\frac{m+n+mn}{mn}$的最小值为5+2$\sqrt{3}$.分析 根据平面向量基本定理求出m,n关系,利用基本不等式的性质进行求解即可.
解答  解:∵$\overrightarrow{AC}$=3$\overrightarrow{AE}$,∴$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$=m$\overrightarrow{AB}$+4n$\overrightarrow{AE}$,
解:∵$\overrightarrow{AC}$=3$\overrightarrow{AE}$,∴$\overrightarrow{AP}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$=m$\overrightarrow{AB}$+4n$\overrightarrow{AE}$,
又∵P为BE上一点,不妨设$\overrightarrow{BP}=λ\overrightarrow{BE}$(0<λ<1),
∴$\overrightarrow{AP}=\overrightarrow{AB}+\overrightarrow{BP}$=$\overrightarrow{AB}$+λ$\overrightarrow{BE}$=$\overrightarrow{AB}$+λ($\overrightarrow{AE}-\overrightarrow{AB}$)=(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AE}$,
∴m$\overrightarrow{AB}$+3n$\overrightarrow{AE}$=(1-λ)$\overrightarrow{AB}$+λ$\overrightarrow{AE}$,
∵$\overrightarrow{AB}$,$\overrightarrow{AE}$不共线,
∴$\left\{\begin{array}{l}{m=1-λ}\\{3n=λ}\end{array}\right.$,则m+3n=1-λ+λ=1,
∴$\frac{m+n+mn}{mn}$=$\frac{m+n}{mn}$+1=$\frac{1}{m}$$+\frac{1}{n}$+1=($\frac{1}{m}+\frac{1}{n}$)×(m+3n)+1
=5+$\frac{3n}{m}$+$\frac{m}{n}$≥5+2$\sqrt{\frac{3n}{m}•\frac{m}{n}}$=5+2$\sqrt{3}$,(m>0,n>0).
当且仅当$\frac{3n}{m}$=$\frac{m}{n}$即m=$\sqrt{3}$n时等号成立,
即$\frac{m+n+mn}{mn}$的最小值为5+2$\sqrt{3}$,
故答案为:5+2$\sqrt{3}$.
点评 本题考查平面向量基本定理和基本不等式求最值,难点在于利用向量求m,n的关系和求m+3n=1.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ |
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 直角三角形 | D. | 上述三种情况都有可能 |
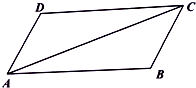 在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,
在平行四边形ABCD中,已知AB=2,AD=1,$\overrightarrow{AB}•\overrightarrow{AC}$=5,