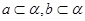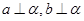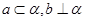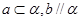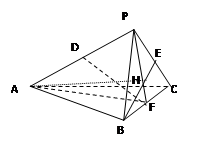题目内容
如图,S是正方形ABCD所在平面外一点,且SD⊥面ABCD ,AB=1,SB=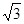 .
.
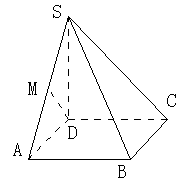
(1)求证:BC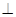 SC;
SC;
(2) 设M为棱SA中点,求异面直线DM与SB所成角的大小
(3) 求面ASD与面BSC所成二面角的大小;
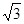 .
.
(1)求证:BC
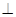 SC;
SC;(2) 设M为棱SA中点,求异面直线DM与SB所成角的大小
(3) 求面ASD与面BSC所成二面角的大小;
(1) 先证BC⊥平面SDC (2) 异面直线DM与SB所成的角为90°(3) 面ASD与面BSC所成
的二面角为45°
的二面角为45°
试题分析:(1)∵底面ABCD是正方形,∴BC⊥DC.
∵SD⊥底面ABCD,∴SD⊥BC,又DC∩SD=D,
∴BC⊥平面SDC,∴BC⊥SC.
(2)取AB中点P,连结MP,DP.
在△ABS中,由中位线定理得MP//SB,
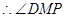 或其补角为所求.
或其补角为所求. ,又
,又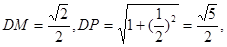
∴在△DMP中,有DP2=MP2+DM2,

即异面直线DM与SB所成的角为90°.

(3).∵SD⊥底面ABCD,且ABCD为正方形,
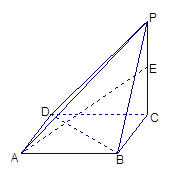
∴可把四棱锥S—ABCD补形为长方体A1B1C1S—ABCD,
如图2,面ASD与面BSC所成的二面角就是面ADSA1与面
BCSA1所成的二面角,
∵SC⊥BC,BC//A1S, ∴SC⊥A1S,
又SD⊥A1S,∴∠CSD为所求二面角的平面角.
在R t△SCB中,由勾股定理得SC=
 ,在R t△SDC中,
,在R t△SDC中,由勾股定理得SD=1.
∴∠CSD=45°.即面ASD与面BSC所成的二面角为45°.
点评:本题考查异面直线垂直的证明,考查异面直线所成角的大小的求法,考查二面角的大小的求法,解题
时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,且
,且 ,
, 为
为 中点.
中点.
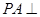 平面
平面 的大小;
的大小; 上是否存在点
上是否存在点 ,使得点
,使得点 的距离为
的距离为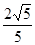 ?若存在,确定点
?若存在,确定点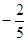
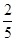
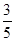
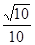
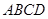 中,
中, ,
, ,点
,点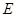 为线段
为线段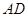 上的一点.现将
上的一点.现将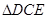 沿线段
沿线段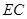 翻折到
翻折到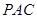 (点
(点 与点
与点 重合),使得平面
重合),使得平面 平面
平面 ,连接
,连接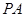 ,
, .
.
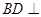 平面
平面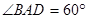 ,且点
,且点 的大小.
的大小.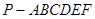 的底面是正六边形,
的底面是正六边形,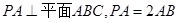 ,则直线
,则直线 所成的角为
所成的角为 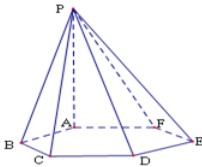
 和
和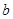 ,必定存在平面
,必定存在平面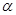 ,使得 ( )
,使得 ( )