题目内容
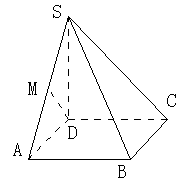
如图所示,四面体ABCD中,AB⊥BD、AC⊥CD且AD =3.BD=CD=2.
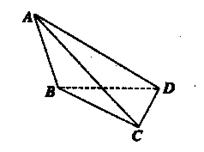
(1)求证:AD⊥BC;
(2)求二面角B—AC—D的余弦值.

(1)求证:AD⊥BC;
(2)求二面角B—AC—D的余弦值.
(1)构造向量证明(2)
试题分析:(1)证明 作AH⊥平面BCD于H,连接BH、CH、DH,

易知四边形BHCD是正方形,且AH=1,以D为原
点,以DB所在直线为x轴,DC所在直线为y轴,
以垂直于DB,
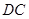 的直线为z轴,建立空间直角坐
的直线为z轴,建立空间直角坐标系,如图所示,则B(2,0,0),C(0,2,0),
 A(2,2,1),
A(2,2,1), 所以
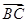 =
= ,
,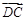 =
=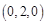
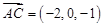 ,
,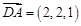
因此
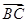 ·
·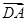 =
=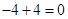 ,所以AD⊥BC.
,所以AD⊥BC. (2)解:设平面ABC的法向量为n1=(x,y,z),则由n1⊥
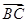 知:n1·
知:n1·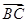 =
=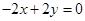
同理由n1⊥
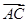 知:n1·
知:n1·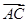 =
=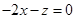 ,
,可取n1=
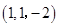 ,
,同理,可求得平面ACD的一个法向量为
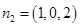
∴
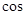 〈n1,n2〉=
〈n1,n2〉=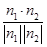 =
=
即二面角B—AC—D的余弦值为
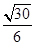
点评:本题考查线面垂直,考查面面角,解题的关键是掌握线面垂直的判定方法,正确运用向量法解决面面角问题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
 是不同的直线,
是不同的直线,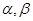 是不同的平面,给出下列五个命题:
是不同的平面,给出下列五个命题: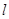 垂直于
垂直于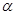 内的两条直线,则
内的两条直线,则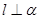 ;
;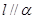 ,则
,则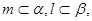 且
且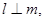 则
则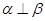 ;
;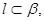 且
且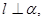 则
则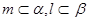 且
且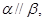 则
则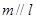 .其中正确命题的序号是
.其中正确命题的序号是  是边长为
是边长为 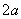 的等边三角形,
的等边三角形, 是分别以
是分别以 为底的全等的等腰三角形,现将该平面图形分别沿
为底的全等的等腰三角形,现将该平面图形分别沿 垂直,连接
垂直,连接 ,得到图二所示的几何体,据此几何体解决下面问题.
,得到图二所示的几何体,据此几何体解决下面问题.
 ;
; 时,求三棱锥
时,求三棱锥 的体积
的体积 ;
; 的余弦值.
的余弦值.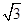 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
 ;
; 为何值时,
为何值时, 与平面
与平面 所成角的大小为45°.
所成角的大小为45°. β且α⊥β,则l⊥α
β且α⊥β,则l⊥α β=m,且l∥m, 则l∥α
β=m,且l∥m, 则l∥α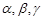 是两两不重合的三个平面,下列命题中错误的是( )
是两两不重合的三个平面,下列命题中错误的是( ) 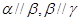 ,则
,则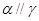
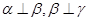 ,则
,则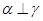
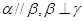 ,则
,则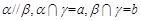 ,则
,则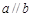
 的正方体
的正方体 中,
中, 分别为
分别为 的中点.
的中点.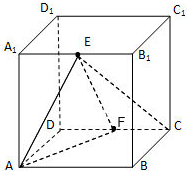
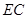 与平面
与平面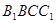 所 成 角的大小;
所 成 角的大小;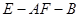 的大小.
的大小.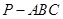 中,
中,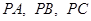 两两垂直,且
两两垂直,且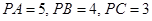 .设点
.设点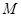 为底面
为底面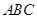 内一点,定义
内一点,定义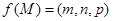 ,其中
,其中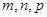 分别为三棱锥
分别为三棱锥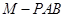 、
、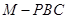 、
、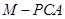 的体积.若
的体积.若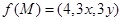 ,且
,且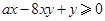 恒成立,则正实数
恒成立,则正实数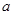 的取值范围是___________.
的取值范围是___________.
 .
.
 SC;
SC;