题目内容
【题目】已知等比数列![]() 的公比
的公比![]() ,前n项和为
,前n项和为![]() .若
.若![]() ,且
,且![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(1)求![]() ;
;
(2)数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的前2019项和;
的前2019项和;
(3)设![]() ,问数列
,问数列![]() 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不存在,理由见解析
;(3)不存在,理由见解析
【解析】
(1)结合等差中项的性质,将已知条件转化为![]() 的形式,由此求得
的形式,由此求得![]() ,进而求得
,进而求得![]() .
.
(2)利用分组求和法求得数列![]() 的前
的前![]() 项和.
项和.
(3)存在![]() ,且
,且![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,根据等差中项的性质列方程,化简后推出矛盾,由此判断出不存在符合条件的项.
成等差数列,根据等差中项的性质列方程,化简后推出矛盾,由此判断出不存在符合条件的项.
(1)由![]() ,得
,得![]() ①.
①.
再由![]() 是
是![]() ,
,![]() 的等差中项,得
的等差中项,得![]() ,
,
即![]() ②.
②.
由①②,得![]() ,
,
即![]() ,亦即
,亦即![]() ,
,
解得![]() 或
或![]() ,又
,又![]() ,故
,故![]() .
.
代入①,得![]() ,
,
所以![]() ,
,
即![]() ;
;
(2)![]()
![]()
![]()
(3)设存在![]() ,且
,且![]() ,使
,使![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
∴![]()
即![]()
∴![]()
∴![]() (*)
(*)
因为![]() 且
且![]()
∴![]() 、
、![]() 为偶数
为偶数
![]() 为奇数,(*)式产生矛盾.所以这样的三项不存在.
为奇数,(*)式产生矛盾.所以这样的三项不存在.

 阅读快车系列答案
阅读快车系列答案【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | 50 |
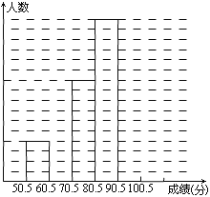
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
【题目】编号分别为![]() 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(1)将得分在对应区间内的人数填入相应的空格:
区间 | [10,20) | [20,30) | [30,40] |
人数 |
(2)从得分在区间[20,30)内的运动员中随机抽取2人.
(ⅰ)用运动员编号列出所有可能的抽取结果;
(ⅱ)求这2人得分之和大于50的概率.