题目内容
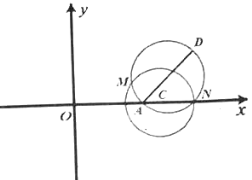
【题目】已知抛物线![]() ,直线
,直线![]() 与E交于A、B两点,且
与E交于A、B两点,且![]() ,其中O为原点.
,其中O为原点.
(1)求抛物线E的方程;
(2)点C坐标为![]() ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为![]() ,证明:
,证明: ![]() 为定值.
为定值.
【答案】(1)![]() ;(2)证明过程详见解析.
;(2)证明过程详见解析.
【解析】试题分析:(1)将直线与抛物线联立,消去y,得到关于x的方程,得到两根之和、两根之积,设出A、B的坐标,代入到![]() 中,化简表达式,再将上述两根之和两根之积代入得到p,从而求出抛物线标准方程.(2)先利用点A,B,C的坐标求出直线CA、CB的斜率,再根据抛物线方程轮化参数y1,y2,得到k和x的关系式,将上一问中的两根之和两根之积代入,化简表达式得到常数即可
中,化简表达式,再将上述两根之和两根之积代入得到p,从而求出抛物线标准方程.(2)先利用点A,B,C的坐标求出直线CA、CB的斜率,再根据抛物线方程轮化参数y1,y2,得到k和x的关系式,将上一问中的两根之和两根之积代入,化简表达式得到常数即可
试题解析:(Ⅰ)将![]() 代入
代入 ![]() ,得
,得![]() .
.
其中![]()
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() .
.
![]() .
.
由已知,![]() ,
,![]() .所以抛物线
.所以抛物线![]() 的方程
的方程![]() .
.
(Ⅱ)由(Ⅰ)知, ![]() ,
,![]() .
.
![]() ,同理
,同理![]() ,
,
所以![]() .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目