Question

【题目】如图，圆的圆心在轴上，且过点，.

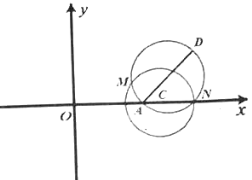
（1）求圆的方程；

（2）直线：与轴交于点，点为直线上位于第一象限内的一点，以为直径的圆与圆相交于点，.若直线的斜率为-2，求点坐标.

Answer 1

【答案】(1) .

(2)

【解析】分析：（1）由题意得到点，连线的垂直平分线，在直线方程中，令可得圆心的坐标，进而可得圆的方程．（2）由题意得，故，根据，得．依题意可设设点坐标为，从而得到直线和的方程，解方程组可得点M的坐标为，由点M在圆上可得的值，从而得到点D的坐标．

详解：（1）由题意可得以点，为端点的线段的中垂线方程为，

令，得，

故圆心为，

所以半径为，

所以圆的方程为．

（2）由为直径，得，

所以，

又直线的斜率为-2，

所以．

设点坐标为，

则直线的方程为，直线的方程为，

即，

解方程组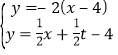可得点M的坐标为．

又点在圆上，

所以

或．

又因为点位于第一象限，

所以点D的坐标为．