题目内容
【题目】已知双曲线![]() 和椭圆
和椭圆![]() 有公共的焦点,且离心率为
有公共的焦点,且离心率为![]() .
.
(Ⅰ)求双曲线![]() 的方程.
的方程.
(Ⅱ)经过点![]() 作直线
作直线![]() 交双曲线
交双曲线![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】试题分析:
(I)设双曲线方程为![]() ,由题意得
,由题意得![]() ,结合
,结合![]() ,可得
,可得![]() ,故可得
,故可得![]() ,
, ![]() ,从而可得双曲线方程。(Ⅱ)由题意知直线
,从而可得双曲线方程。(Ⅱ)由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,与双曲线方程联立消元后根据根与系数的关系可得
,与双曲线方程联立消元后根据根与系数的关系可得![]() ,解得
,解得![]() 可得直线方程。
可得直线方程。
试题解析:
(I)由题意得椭圆![]() 的焦点为
的焦点为![]() ,
, ![]() ,
,
设双曲线方程为![]() ,
,
则![]() ,
,
∵![]()
∴![]() ,
,
∴ ![]() ,
,
解得![]() ,
,
∴ ![]() ,
,
∴ 双曲线方程为![]() .
.
(II)由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,即
,即![]() 。
。
由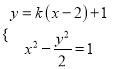 消去x整理得
消去x整理得
![]() ,
,
∵直线![]() 与双曲线交于
与双曲线交于![]() ,
, ![]() 两点,
两点,
∴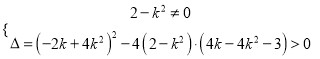 ,
,
解得![]() 。
。
设![]() ,
, ![]() ,
,
则![]() ,
,
又![]() 为
为![]() 的中点
的中点
∴ ![]() ,
,
解得![]() .满足条件。
.满足条件。
∴ 直线![]() ,即
,即![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中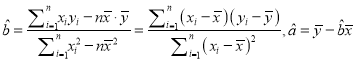 .
.