题目内容
地面上有三个同心圆(如右图), 其半径分别为3、2、1。若向图中最大的圆内投点且投到图中阴影区域的概率为 ,则两直线所夹锐角的弧度数为 。
,则两直线所夹锐角的弧度数为 。

解析试题分析:设两直线所夹锐角弧度为α,则有: ,
,
解得:α= .故答案为
.故答案为 。
。
考点:本题主要考查几何概型概率的计算,弧度制。
点评:简单题,解题的关键是明确两个几何区域的“几何度量”,即找出:“两直线所夹锐角”对应图形的面积,及整个图形的面积,按概率计算公式,计算比值。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,直线
,直线 :
: 和曲线
和曲线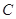 :
: 有两个不同的交点,直线
有两个不同的交点,直线 ,向区域Ω内随机投一点A,点A落在区域
,向区域Ω内随机投一点A,点A落在区域 ,若
,若 ,则实数
,则实数 的取值范围是________。
的取值范围是________。 ,
, 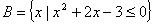 ,在集合
,在集合 中任意取一个元素
中任意取一个元素 ,则
,则 的概率是 .
的概率是 . 的值介于0到0.5之间的概率为 .
的值介于0到0.5之间的概率为 . 的值为 .(精确到0.01)
的值为 .(精确到0.01)
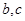 ,则方程
,则方程 有实根的概率为
有实根的概率为  内任取一点P,则点P落在单位圆
内任取一点P,则点P落在单位圆 内的概率为 .
内的概率为 .