题目内容
将一枚骰子抛掷两次,若先后出现的点数分别为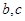 ,则方程
,则方程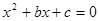 有实根的概率为
有实根的概率为

解析试题分析:将一枚骰子抛掷两次,若先后出现的点数分别为b,c,共有36种结果:(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),
(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),
(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),
(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),属于古典概型.
记“方程x2+bx+c=0有实根”为事件A,则△=b2-4c≥0即b≥2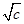 ,A包含的结果有:(2,1),(3,1)(4,1),(5,1),(6,1),(3,2),(4,2),(5,2),(6,2),(4,3),(5,3),
,A包含的结果有:(2,1),(3,1)(4,1),(5,1),(6,1),(3,2),(4,2),(5,2),(6,2),(4,3),(5,3),
(6,3),(4,4),(5,4),(6,4),(5,5),(6,5),(5,6),(6,6)共19种结果,由古典概率的计算公式可得,P(A)= 。
。
考点:本题主要考查古典概型概率的计算。
点评:中档题,此类型题的求解有两点:①首先清楚古典概率模型的特征:结果有限且每种结果等可能出现②古典概率的计算公式:P(A)=m/n(其中n是试验的所有结果,m是基本事件的结果数.)难点在确定“结果数”。

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 (各学校是否录取他相互独立,允许他可以被多个学校同时录取).则此同学至少被两所学校录取的概率为_____.
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).则此同学至少被两所学校录取的概率为_____. ,则两直线所夹锐角的弧度数为 。
,则两直线所夹锐角的弧度数为 。
 ,则他在3天乘车中,此班次公共汽车至少有2天准时到站的概率为
,则他在3天乘车中,此班次公共汽车至少有2天准时到站的概率为  AB的长度小于1的概率为 ;
AB的长度小于1的概率为 ; ,在区间
,在区间 上随机取一个数
上随机取一个数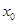 ,则使得
,则使得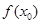 ≥0的概率为 .
≥0的概率为 . ,则该菱形内的点到点A、B的距离均不小于1的概率是
,则该菱形内的点到点A、B的距离均不小于1的概率是