题目内容

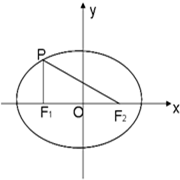
如图，F1，F2是椭圆
x2
a2
+
y2
b2
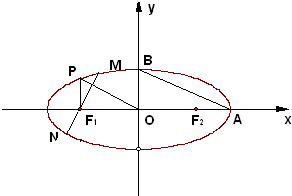
=1（a＞b＞0）上的焦点，P为椭圆上的点，PF1⊥OX轴，且OP和椭圆的一条长轴顶点A和短轴顶点B的连线AB平行．
（1）求椭圆的离心率e
（2）若Q是椭圆上任意一点，证明∠F1QF2≤
π
2

（3）过F1与OP垂直的直线交椭圆于M，N，若△MF2N的面积为20
3
，求椭圆方程．
（1）易得 P(-c，
b2
a
)，kOP=
b2
-ac
，kAB=-
b
a
，
∴-
b2
ac
=-
b
a
⇒b=c⇒a=
2
c，
∴e=
c
a
=
2
2
．
（2）证明：由椭圆定义得：|F1Q|+|F2Q|=2a，
所以cos∠F1QF2=
|F1Q|2+|F2Q|2-|F1F2|2
2|F1Q||F2Q|

=
4a2-4c2-2|F1Q||F2Q|
2|F1Q||F2Q|
=
2b2
|F1Q||F2Q|
-1，
因为|F1Q||F2Q|≤(
|F1Q|+|F2Q|
2
)2=a2，
∴cos∠F1QF2≥
2b2
a2
-1=
2c2
2c2
-1=0，
∴∠F1QF2≤
π
2
．
（3）设直线MN的方程为 y=
a
b
（x+c），即y=
2
(x+c)．
代入椭圆方程消去x得：
(1-
1
2
y+c)2
a2
+
y2
b2
=1，
整理得：5y2-2
2
cy-2c2=0，
∴y1+y2=
2
2
c
5
，y1•y2=-
2c2
5
．
∴(y1-y2)2=(
2
2
c
5
)2+
8c2
5
=
48c2
25
．
因为S△PF2Q=
1
2
•2c•|y1-y2|=
4
3
c2
5
=20
3
，
所以c2=25
因此a2=50，b2=25，
所以椭圆方程为
x2
50
+
y2
25
=1．
练习册系列答案
相关题目
已知椭圆C与双曲线
x2
2
-
y2
6
=1有相同焦点F1和F2，过F1的直线交椭圆于A、B两点，△ABF2的周长为8
3
．若直线y=t（t＞0）与椭圆C交于不同的两点E、F，以线段EF为直径作圆M．
（1）求椭圆C的标准方程；
（2）若圆M与x轴相切，求圆M被直线x-
3
y+1=0截得的线段长．
已知点P（-1，
3
2
）是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）上一点，F1、F2分别是椭圆C的左、右焦点，O是坐标原点，PF1⊥x轴．
①求椭圆C的方程；
②设A、B是椭圆C上两个动点，满足
PA
+
PB
=λ
PO
（0＜λ＜4，且λ≠2）求直线AB的斜率．
以椭圆
x2
16
+
y2
4
=1内的点M（1，1）为中点的弦所在直线方程为______．
椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点为F1，F2，点P在椭圆C上，且PF1⊥F1F2，|PF1|=
4
3
，|PF2|=
14
3
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若直线l过点M（-2，1），交椭圆C于A，B两点，且M恰是A，B中点，求直线l的方程．
设双曲线方程
x2
a2
-
y2
b2
=1(b＞a＞0)的半焦距为c，直线l过（a，0），（0，b）两点，已知原点到直线l的距离为
3
4
c．
（1）求双曲线的离心率；
（2）经过该双曲线的右焦点且斜率为2的直线m被双曲线截得的弦长为15，求双曲线的方程．
已知直线l：y=3x+2过抛物线y=ax2（a＞0）的焦点．
（1）求抛物线方程；
（2）设抛物线的一条切线l1，若l1∥l，求切点坐标．
椭圆C1：
x2
a2
+
y2
b2
=1(a＞b＞0)与抛物线C2：x2=2py（p＞0）的一个交点为M．抛物线C2在点M处的切线过椭圆C1的右焦点F．
（1）若M(2，
2
5
5
)，求C1和C2的标准方程；
（II）若b=1，求p关于a的函数表达式p=f（a）．
双曲线x2-y2=a2截直线4x+5y=0的弦长为
41
，则此双曲线的实轴长为（　　）
A．3B．
3
2
C．
12
5
D．
6
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网