题目内容
【题目】已知椭圆
＋
＝1(a>b>0)的左焦点为F，右顶点为A，抛物线y2＝
(a＋c)x与椭圆交于B，C两点，若四边形ABFC是菱形，则椭圆的离心率等于( )
A. B. 
C. 
D. 
【答案】D
【解析】∵椭圆
＋
＝1(a>b>0)的左焦点为F，右顶点为A，∴A(a，0)，F(－c，0)．
∵抛物线y2＝
(a＋c)x与椭圆交于B，C两点，
∴B，C两点关于x轴对称，可设B(m，n)，C(m，－n)．
∵四边形ABFC是菱形，
∴m＝
(a－c)．
将B(m，n)代入抛物线方程，得
n2＝ (a＋c)· (a－c)＝
b2，
∴B
，再代入椭圆方程，得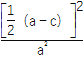
＋
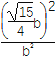＝1，
即
·
＝
，
化简整理，得4e2－8e＋3＝0，解得e＝ (e＝
>1不符合题意，舍去)．故选D.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
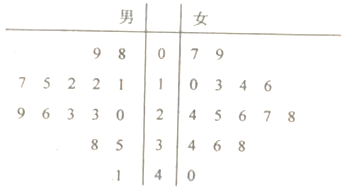
【题目】某数学教师对所任教的两个班级各抽取20名学生进行测试，分数分布如表：
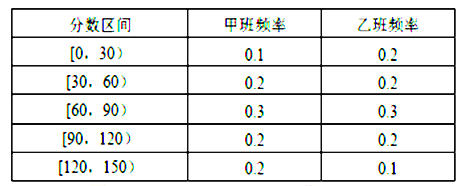
（1）若成绩120分以上（含120分）为优秀，求从乙班参加测试的90分以上（含90分）的同学中，随机任取2名同学，恰有1人为优秀的概率；
（2）根据以上数据完成下面的
列联表：在犯错概率小于
的前提下，你是否有足够的把握认为学生的数学成绩是否优秀与班级有关系？
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
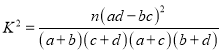，其中
.
