题目内容
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ),
),![]() (
(![]() ,
,![]()
![]() ),
),
⑴若![]() ,
,![]() .求
.求![]() 在
在![]() 上的最大值
上的最大值![]() 的表达式;
的表达式;
⑵若![]() 时,方程
时,方程![]() 在
在![]() 上恰有两个相异实根,求实根
上恰有两个相异实根,求实根![]() 的取值范围;
的取值范围;
⑶若![]() ,
,![]() ,求使
,求使![]() 得图像恒在
得图像恒在![]() 图像上方的最大正整数
图像上方的最大正整数![]() .
.
【答案】(1)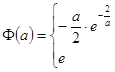
![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)借助题设条件运用分类整合思想求解;(2)依据题设运用化归转化的数学思想进行探求;(3)依据题设构造函数![]() ,运用导数的知识求解.
,运用导数的知识求解.
试题解析:
(1)![]() 时,
时,![]() ,
,
![]() ;
;
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,此时
上为增函数,此时![]() ,
,
②当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,
故![]() 在
在![]() 上为增函数,此时
上为增函数,此时![]() …………………………………2分
…………………………………2分
③当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,
若![]() ,即
,即![]() 时,故
时,故![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,
上为减函数,
此时![]() ………………………………5分
………………………………5分
若![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上为增函数,则此时
上为增函数,则此时![]() ,
,
综上所述: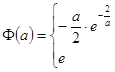
![]() ………………………………6分,
………………………………6分,
(2)![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,……………7分
上单调递增,……………7分
![]()
![]() 在
在![]() 上恰有两个相异实根,
上恰有两个相异实根,
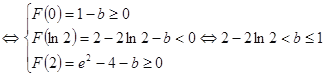 ,
,
![]() 实数
实数![]() 的取值范围是
的取值范围是![]() ,…………………………………10分
,…………………………………10分
(3)由题设:![]() ,
,![]() ,(*)
,(*)
![]() ,故
,故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() (*)
(*)![]() ,
,
设![]() ,则
,则![]() ,
,
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,…………………………12分
上单调递减,…………………………12分
而![]() ,
,
且![]() ,
,
故存在![]() ,使
,使![]() ,
,
且![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,
又![]() ,
,![]() ,
,![]() 时,使
时,使![]() 的图像恒在
的图像恒在![]() 图像的上方的最大整数
图像的上方的最大整数![]() ………………14分.
………………14分.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目