题目内容
【题目】已知长方形ABCD中,AB=1,AD=![]() 。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
。现将长方形沿对角线BD折起,使AC=a,得到一个四面体ABCD,如图所示.
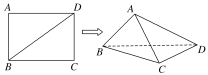
(1)试问:在折叠的过程中,异面直线AB与CD,AD与BC能否垂直?若能垂直,求出相应的a值;若不垂直,请说明理由.
(2)当四面体ABCD的体积最大时,求二面角ACDB的余弦值.
【答案】见解析
【解析】
解:(1)若AB⊥CD,因为AB⊥AD,AD∩CD=D,
所以AB⊥平面ACD,所以AB⊥AC.
即AB2+a2=BC2,即12+a2=(![]() )2,所以a=1。
)2,所以a=1。
若AD⊥BC,因为AD⊥AB,
所以AD⊥平面ABC,所以AD⊥AC.
即AD2+a2=CD2,即(![]() )2+a2=12,
)2+a2=12,
所以a2=-1,无解.
故AD⊥BC不成立.
(2)要使四面体ABCD的体积最大,因为△BCD的面积为定值![]() ,
,
所以只需三棱锥ABCD的高最大即可,此时平面ABD⊥平面BCD,
过点A作AO⊥BD于点O,
则AO⊥平面BCD,
以O为坐标原点建立空间直角坐标系Oxyz(如图),

则易知A![]() ,C(
,C(![]() ,
,![]() ,0),D
,0),D![]() ,
,
显然,平面BCD的一个法向量为![]() =
=![]() 。
。
设平面ACD的法向量为n=(x,y,z).
因为![]() =
=![]() ,
,![]() =
=![]() ,
,
所以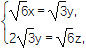 令y=
令y=![]() ,得n=(1,
,得n=(1,![]() ,2).
,2).
故二面角ACDB的余弦值为|cos〈![]() ,n〉|=
,n〉|=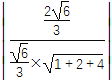 =
=![]() 。
。

练习册系列答案
相关题目