题目内容
11.已知函数y=ax3-x在(-1,1)上是单调减函数,则实数a的取值范围( )| A. | a<$\frac{1}{3}$ | B. | a=1 | C. | a=$\frac{1}{3}$ | D. | a≤$\frac{1}{3}$ |
分析 根据函数单调性和导数之间的关系进行求解.
解答 解:若函数y=ax3-x在(-1,1)上是单调减函数,
则y′≤0在(-1,1)上恒成立,
即3ax2-1≤0在(-1,1)上恒成立,
即3ax2≤1,
若a≤0,满足条件.
若a>0,则只要当x=1或x=-1时,满足条件即可,
此时3a≤1,即0<a≤$\frac{1}{3}$,
综上a≤$\frac{1}{3}$,
故选:D.
点评 本题主要考查函数单调性的应用,利用导数和函数单调性的关系转化为f′(x)≤0恒成立是解决本题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
1.从装有红球、黑球和白球的口袋中摸出一个球,若摸出的球是红球的概率是0.4,摸出的球是黑球的概率是0.25,那么摸出的球是白球或黑球的概率是( )
| A. | 0.35 | B. | 0.65 | C. | 0.1 | D. | 0.6 |
16.已知8件产品中有2件次品,从中任取3件,取到次品的件数为随机变量,用ξ表示,那么ξ的取值为( )
| A. | 0,1 | B. | 1,2 | C. | 0,1,2 | D. | 0,1,2,3 |
1. 辛集中学高二学生要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.恰有两个区域用红色鲜花的概率( )
辛集中学高二学生要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.恰有两个区域用红色鲜花的概率( )
 辛集中学高二学生要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.恰有两个区域用红色鲜花的概率( )
辛集中学高二学生要用鲜花布置花圃中ABCDE五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.恰有两个区域用红色鲜花的概率( )| A. | $\frac{8}{35}$ | B. | $\frac{6}{35}$ | C. | $\frac{4}{35}$ | D. | $\frac{2}{35}$ |
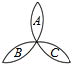 荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是$\frac{1}{3}$.
荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示,假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是$\frac{1}{3}$.