题目内容
19.若不等式0≥sin2x+mcosx-2对任意x∈[0,$\frac{1}{2}$π)恒成立,求m的取值范围.分析 问题等价于m小于等于f(x)=$\frac{2-si{n}^{2}x}{cosx}$在x∈[0,$\frac{1}{2}$π)时的最小值,由三角函数和基本不等式可得.
解答 解:∵不等式0≥sin2x+mcosx-2对任意x∈[0,$\frac{1}{2}$π)恒成立,
∴mcosx≤2-sin2x对任意x∈[0,$\frac{1}{2}$π)恒成立,
∴m≤$\frac{2-si{n}^{2}x}{cosx}$对任意x∈[0,$\frac{1}{2}$π)恒成立,
∴只需m小于等于f(x)=$\frac{2-si{n}^{2}x}{cosx}$在x∈[0,$\frac{1}{2}$π)时的最小值,
变形可得f(x)=$\frac{2-(1-co{s}^{2}x)}{cosx}$=$\frac{1+co{s}^{2}x}{cosx}$
=$\frac{1}{cosx}$+cosx≥2$\sqrt{\frac{1}{cosx}•cosx}$=2,
当且仅当$\frac{1}{cosx}$=cosx即cosx=1即x=0时取等号,
∴m的取值范围为(-∞,2]
点评 本题考查三角函数的最值,涉及恒成立和基本不等式,属中档题.

练习册系列答案
相关题目
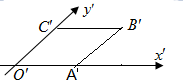 已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )
已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )