题目内容
14.如图,一长为$\sqrt{3}$dm,宽为1dm的长方形木块在桌面上作无滑动翻滚,翻滚到第三面时被一小木板挡住,使木块底面与桌面成30°的角,则点A走过的弧的总长为$\frac{(9+2\sqrt{3})π}{6}$dm.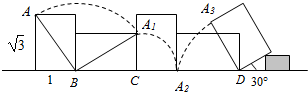
分析 由弧长公式计算各段弧长,相加可得.
解答 解:由题意可得第一段弧长AA1=$\frac{π}{2}$×2=π,
第二段弧长A1A2=$\frac{π}{2}$×1=$\frac{π}{2}$,
第三段弧长A2A3=$\frac{π}{3}$×$\sqrt{3}$=$\frac{\sqrt{3}π}{3}$,
∴点A走过的弧的总长为π+$\frac{π}{2}$+$\frac{\sqrt{3}π}{3}$=$\frac{(9+2\sqrt{3})π}{6}$,
故答案为:$\frac{(9+2\sqrt{3})π}{6}$.
点评 本题考查弧长公式,求出各段弧长的圆心角和半径是解决问题的关键,属基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
2.定义域为R的函数f(x)对任意的x都有f(2+x)=f(2-x),且其导函数f′(x)满足:$\frac{f′(x)}{2-x}$>0,则当2<a<4时,下列成立的是( )
| A. | f(log2a)<f(2)<f(2a) | B. | f(2a)<f(log2a)<f(2) | C. | f(2a))<f(2)<f(log2a) | D. | f(log2a)<f(2a)<f(2) |
3.已知F为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的一个焦点,A1、A2为椭圆长轴的两个端点,P为椭圆上任一点,分别以PF、A1A2为直径作圆,则两圆的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 内含 |
4.下列函数在区间(-∞,0)上为增函数的是( )
| A. | y=x2 | B. | y=$\frac{-2}{x}$ | C. | y=($\frac{1}{2}$)x | D. | y=3-x |