题目内容

3．△ABC中，三内角A，B，C成等差数列，对应三边a，b，c成等比数列，则此三角形是（　　）
A．等腰直角三角形B．等边三角形C．等腰三角形D．直角三角形

分析 由等差数列和等比数列的性质，可得B=60°，b2=ac，再由余弦定理可得a=c，即可判断三角形的形状．

解答 解：三内角A，B，C成等差数列，
即有A+C=2B，又A+B+C=180°，
可得B=60°，
由余弦定理可得b2=a2+c2-2accos60°
=a2+c2-ac，
由对应三边a，b，c成等比数列，
可得b2=ac，
即有a2+c2-2ac=0，即为a=c，
故△ABC为等边三角形．
故选B．

点评 本题考查等差数列和等比数列的性质，考查余弦定理和三角形内角和定理的运用，属于中档题．

练习册系列答案
相关题目
13．若f（x+1）=x2+2x+2，则f（2）=5．
14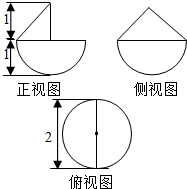．某几何体的三视图如图所示．则该几何体的体积为（　　）
A．πB．$\frac{3π}{2}$C．$\frac{5π}{3}$D．$\frac{5π}{6}$
11．一个动点到直线x=8的距离是它到点A（2，0）的距离的2倍，求动点的轨迹方程．
18．阅读理解：如图，A、B、C为数轴上三点，若点C到A的距离是点C到B的距离的2倍，我们就称点C是[A，B]的好点．例如，如图1，点A表示的数为-1，点B表示的数为2．表示数1的点C到点A的距离是2，到点B的距离是1，那么点C是[A，B]的好点；又如，表示数0的点D到点A的距离是1，到点B的距离是2，那么点D就不是[A，B]的好点，但点D是[B，A]的好点．

知识运用：如图2，M、N为数轴上两点，点M所表示的数为-2，点N所表示的数为4．
（1）数2或10所表示的点是[M，N]的好点；
（2）现有一只电子蚂蚁P从点N出发，以每秒2个单位的速度沿数轴向左运动，运动时间为t．当t为何值时，P、M、N中恰有一个点为其余两点的好点？
8．设曲线y=ax+ln（x+1）在点（0，0）处的切线方程为y=x，则a=（　　）
A．0B．1C．2D．3
15．已知球O的体积等于$\frac{125π}{6}$，如果长方体的八个顶点都在球O的球面上，那么这个长方体的表面积的最大值等于50．
12．已知p：-2≤x≤5，q：m+1≤x≤2m-1，若q是p的充分条件，求实数m的取值范围．
13．已知函数f（x）=$\sqrt{3}$（cos$\frac{x}{2}$-sin$\frac{x}{2}$）（cos$\frac{x}{2}$+sin$\frac{x}{2}$）+2sin$\frac{x}{2}$cos$\frac{x}{2}$．
（1）求f（x）的最小正周期；
（2）若将f（x）的图象先向左平移$\frac{π}{6}$个单位，再把图象上各点的横坐标变为原来的$\frac{2}{π}$倍，纵坐标不变，得到函数g（x）的图象，数列{an}满足an=g（n），记数列{an}的前n项和为Sn，求S17．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网